1.9. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО ТЕМЕ «УСЛОВНЫЕ ВЫРАЖЕНИЯ И ВЕТВЯЩИЕСЯ АЛГОРИТМЫ»

Вариант 1

         Составить блок-схему и программу на языке Фортран для решения следующих задач.

1. Даны три действительных числа. Выбрать и напечатать те из них, которые принадлежат интервалу (1, 3).
2. Если сумма трех попарно различных действительных чисел х, у, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других, в противном случае заменить меньшее из х и у полусуммой двух оставшихся значений.
3. Даны четыре действительных числа, вычислить .

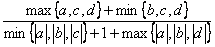Вариант 2

         Составить блок-схему и программу на языке Фортран для решения следующих задач.

1. Даны действительные числа х, y (х не равно y). Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением.
2.  Даны действительные – числа .a, b, с, d. Если 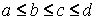, то каждое число  заменить наибольшим из них ; если a>b>c>d,  то числа оставить без изменения; в противном случае все числа заменяются их квадратами.
3. Четырехугольник задан координатами своих вершин. Проверить, является ли этот четырехугольник трапецией.

Вариант 3

     Составить блок-схему и программу на языке Фортран для решения следующих задач.

1. Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
2. Даны действительные положительные числа x, y, z. Выяснить, существует ли треугольник с длинами сторон x, y, z. Если треугольник существует, то ответить, является ли он остроугольным.
3. Дано действительное число h. Выяснить, имеет ли yравнение ax²+bx+c=0 действительные корни, если 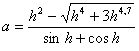   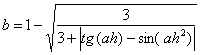, , 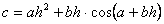. Если действительные корни существуют, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.

 Вариант 4

         Составить блок-схему и программу на языке Фортран для решения следующих задач.

1. Четырехугольник задан координатами своих сторон. Проверить, можно ли в этот четырехугольник вписать окружность, описать около него окружность.
2.  Даны действительные числа х, у. Если х и у отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0.5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0,5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях х и y оставить без изменения. 
3. Даны действительные числа а, b, с  (а не равно 0). Выяснить, имеет ли уравнение ax²+bx+c=0 действительные корни. Если действительные корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
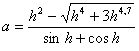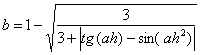