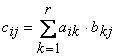Можно выделить следующие этапы модельного исследования:

ü  постановка задачи;

ü  построение модели, исследование объекта и составление его математического описания;

ü  отыскание решения, построение алгоритма, моделирующего поведение объекта;

ü  контроль правильности результатов и их внедрение.

Построение модели представляет собой не однократный акт, а процесс последовательных уточнений. Подобный итерационный характер построения модели есть принципиальное свойство процесса моделирования. Необходимо отметить тот факт, что успешное моделирование зависит от полноты представлений об объекте, его связях, свойствах, процессах, в которых он участвует. Поэтому при проведении модельных исследований важно хорошо представлять объектную область. При проведении численных экспериментов большую роль играет алгоритм и программа, реализующая алгоритм. Важная характеристика алгоритма – вычислительная сложность – напрямую связана с расчетным временем.

2.2.2. Вычислительная сложность алгоритма

Оценку вычислительной сложности алгоритмов можно выполнять по числу арифметических операций, необходимых для получения результата. При работе с вещественными данными выполняются операции с плавающей точкой, каждую из которых принято называть флопом (от floating point operation). Таким образом, общая трудоемкость задачи оценивается числом выполненных при ее решении флопов.

ПРИМЕРЫ:

1) сложение двух векторов размера n требует п флопов;

2) скалярное произведение двух векторов размера n требует 2n флопов(n сложений и n умножений);

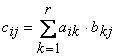3) в случае вложенных циклов суммируют обычно флопы наиболее глубоко вложенных операторов. Так, при умножении матриц  получается матрица Þ. Наиболее глубоко вложенным является оператор c(i,j) = c(i,j) +a(i, k)*b(k,j), который содержит 2 флопа и выполняется при умножении матриц общего вида тпr раз. То есть оценка трудоемкости такого умножения равна 2mnr флопам.