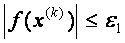 и
и
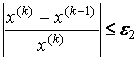 . Процесс
останавливается, если выполняется хотя бы одно из этих условий.
. Процесс
останавливается, если выполняется хотя бы одно из этих условий. При поиске вещественных корней на отрезке изоляции в библиотеке IMSL применяются гибридные алгоритмы, включающие метод половинного деления, метод секущих и обратную квадратичную интерполяцию. В качестве критерия останова итерационного процесса в процедурах IMSL используются критерии
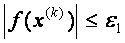 и
и
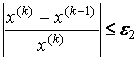 . Процесс
останавливается, если выполняется хотя бы одно из этих условий.
. Процесс
останавливается, если выполняется хотя бы одно из этих условий.
Рассмотрим подпрограмму ZBREN, которая выполняет поиск вещественного корня на заданном отрезке. Эта подпрограмма имеет вызов CALL ZBREN(f,eps1,eps2, a, b, maxf).
Параметры подпрограммы ZBREN:
f – имя вещественной внешней функции одного вещественного аргумента, нуль которой нужно найти. Функция должна обладать атрибутом EXTERNAL. Ее аргумент не должен изменяться в теле функции.
eps1- входной параметр
вещественного типа, используется как критерий завершения вычисления.
Принимается корень b, если ![]() eps1.
Можно задавать eps1=0.
eps1.
Можно задавать eps1=0.
eps2- входной параметр вещественного типа, используется как критерий останова. Корень принимается если относительная разница между приближениями, найденными в двух последних итерациях, меньше eps2.
a, b – входные/выходные параметры вещественного типа: на входе - начало и конец отрезка изоляции. На выходе b содержит найденный корень.
maxfn - входной/выходной параметр целого типа. На входе задает максимально допустимое число вычислений функции, на выходе содержит число вызовов, потребовавшихся для решения задачи.
ПРИМЕР: Вычислить корни уравнения ![]() 0.
0.
РЕШЕНИЕ. Для решения задачи, составим программу на языке Фортран, в которой будем использовать процедуру ZBREN. Как отмечалось выше, это уравнение имеет два корня. Для первого корня зададим отрезок изолированности - [-1.0; -0.5], а для второго – [0.5; 1.0] (см. график функции). Положим значения eps1=0.0 eps2=0.0001. Максимально допустимое число вычислений функции maxfn=100. Выведем на печать приближенное значение корня, число вызовов функции и значение функции в точке корня.
ЗАДАНИЕ:
1) Применить программу (ZBREN.exe) для проведения численного эксперимента, задавая
следующие значения:
для проведения численного эксперимента, задавая
следующие значения:
2) Проанализировать результаты численного эксперимента: изменение значений корня, значения функции в точке корня и числа вызовов функции, потребовавшихся для решения задачи.