, К численным методам алгебры относятся
ü методы нахождения собственных значений и векторов матриц;
ü численные методы решения систем линейных уравнений(СЛАУ);
ü методы обращения матриц;
ü вычисления определителей.
Формально решение этих задач не встречает трудностей: например, если требуется решить СЛАУ
,
где A квадратная матрица порядка m,
m -мерный вектор неизвестных,
а 
вектор
свободных членов. Для решения задачи можно применить правило
Крамера, согласно которого: если определитель системы отличен от нуля, то
система имеет единственное решение
,
определитель матрицы 
, 
определитель матрицы 
, которая получается из
матрицы заменой
го столбика
столбцом свободных членов. Далее для вычисления определителей можно воспользоваться
теоремой Лапласа: если в определители 
го порядка произвольно выбраны 
строк (или столбцов) и 
, тогда сумма
произведений всех миноров 
-го порядка на их алгебраические
дополнения равна определителю 
. При таком подходе для получения решения
СЛАУ потребуется выполнить 
операций. Однако требуемое для решения
число операций нарастает с увеличением порядка системы. Так при значении 
число операций,
которое необходимо выполнить примерно равно 
, возникает вопрос насколько это большое
число операций и каким должно быть быстродействие ЭВМ, для того чтобы задача
была решена за реальное время.
Для ответа на
этот вопрос рассмотрим гипотетическую ЭВМ[Бахвалов Н.С. Численные методы],
которая занимает объем 
, пусть эта машина с параллельно
работающими процессорами, каждый из которых представляет куб c
размером ребра 
,
т.к. скорость передачи сигнала не превосходит скорости света, то минимальное
время выполнения одной операции 
, где 
. За одну секунду общее число операций,
которое выполняется такой ЭВМ равно числу элементов умноженному на время
выполнения одной операции 
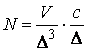. Простые расчеты показывают, что если
представить гипотетическую ЭВМ размера солнечной системы, полностью забитую
параллельно работающими процессорами, и в каждом таком процессоре обмены
происходят со скоростью света, то для решения системы из 100 уравнений со ста
неизвестными недостаточно 15 миллиардов лет.
В вычислительной алгебре разработаны численные методы которые позволяют решать системы с очень большим числом уравнений.
Методы решения алгебраических задач подразделяются на точные, итерационные и вероятностные.
Метод решения относится к классу точных, если в предположении отсутствия округления он дает точное решение задачи после конечного числа арифметических и логических операций.
Метод решения относится к классу итерационных, если решение находится, как предел последовательных приближений к искомому решению.
Метод решения называется вероятностным, если для получения решения привлекаются теоретико-вероятностные представления.