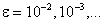1.4. Значащие цифры и верные значащие цифры числа

При решении различных прикладных задач часто ставится условие получить результат с определенной точностью ε, например 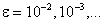Что это значит? Точность вычисления в вычислительной математике определяется количеством цифр результата, заслуживающих доверия, а не числом десятичных знаков после запятой (см. [1, с. 34–35]).

Известно, что любое число можно представить в виде конечной или бесконечной дроби

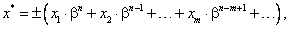(1.7)

где – цифры числа , – основание системы счисления, причем , – некоторое целое число (старший разряд числа ).

Если , то, например, для числа 327,012… можно записать представление

.

В основном на практике имеют дело с приближенными числами – конечными дробями. Пусть . Тогда, например, для числа , состоящего из m цифр, имеет место такое представление:

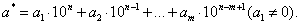(1.8)

Все сохраняемые десятичные знаки называются значащими цифрами числа , среди них есть равные нулю, за исключением .

Итак, значащими цифрами числа называют все цифры в его представлении, начиная с первой отличной от нуля слева.

Если при записи числа 237000 надо показать, что три последних нуля не являются значащими цифрами, то пишут это число следующим образом:

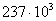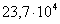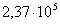, или , или , или .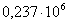

Абсолютные и относительные погрешности для приближенных вещественных чисел тесно связаны с очень важным понятием верных значащих цифр (см. [1, c. 34–35]).

Говорят, что число 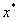имеет 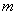 верных значащих цифр, если для абсолютной погрешности числа 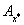справедливо неравенство

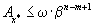(1.9)

где

.

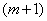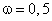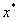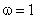-я цифра числа считается сомнительной. В случае, когда (1.9) выполняется при , говорят о верных значащих цифрах числа  в узком смысле слова, а когда , то в широком смысле.

Если 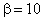, то получим, что

.
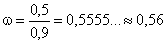