1.5. Неустранимая погрешность функции
В теории погрешностей рассматриваются две основные задачи: прямая и обратная. Сформулируем эти задачи и укажем способы их решения (см. [1, c. 37–45]; [2, c. 41–46]; [3, c. 30]).
Прямая задача. Пусть задана функция
Требуется, зная приближенные
значения аргументов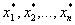 
и
их абсолютные погрешности 
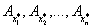, оценить неустранимую погрешность функции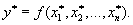 
Будем решать поставленную задачу при следующих предположениях:
1) 
где G – некоторая выпуклая область n-мерного
числового пространства;
2) погрешности
, 
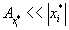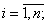
3) погрешность
приближенного значения функции 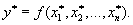требуется найти с небольшой точностью,например, один-два верных знака.
Сформулированные предположения позволяют сократить объем вычислений погрешности функции. В самом деле, по формуле конечных приращений Лагранжа имеем
 |
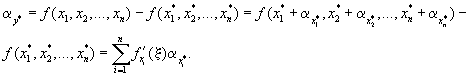(1.10) |
Здесь 
– производные функции, вычисленные в точке 
отрезка,
соединяющего точки 
и
. Координаты
точки ξ неизвестны. Однако в силу второго предположения о малости
погрешностей аргументов функции мы можем заменить точку ξ на 
. Тогда из формулы (1.10)
получаем
 |
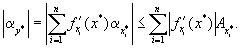(1.11) |
Можно подобрать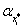 
таким образом, что правая
часть неравенства (1.11) будет равна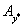 
.
Следовательно,
предельная абсолютная погрешность приближенного значения функции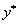 
вычисляется по формуле
 |
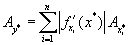(1.12) |
Тогда, используя определение предельной
относительной погрешности приближенного значения ,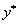
получаем формулу для её нахождения
 |
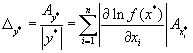(1.13) |
Можно выразить относительную погрешность функции через относительные погрешности аргументов. В этом случае формула (1.13) примет вид
 |
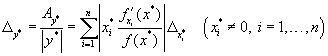(1.14) |
Итак, формулы (1.12) – (1.14) дают общие выражения для абсолютной и относительной погрешности функции, зависящей от нескольких приближенных аргументов, при сформулированных выше трёх предположениях. Применение формул (1.12) – (1.14) в некоторых частных случаях даёт интересные результаты (см. [1, с. 39–42]; [2, c. 31–40];[3, c. 16–19]). Приведём их.
Погрешность суммы. Рассмотрим
, где 
.
Так как все 
, то согласно формуле (1.12) получаем
 |
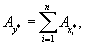(1.15) |
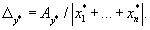
Другими словами, при сложении приближённых величин их абсолютные погрешности складываются.
Заметим, что формула
(1.15) даёт сильно завышенное значение абсолютной погрешности, если число
слагаемых n велико, т.к.
обычно погрешности имеют разные знаки и при их сложении происходит частичная
компенсация. В таких случаях можно пользоваться правилом статистической оценки
абсолютной погрешности суммы (см. [5, с. 12]). Если
погрешности всех слагаемых оцениваются величиной 
, т.е. слагаемые округлены до p-го десятичного разряда, то по правилу статистической
оценки
 |
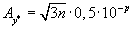