1.6. Вычислительная погрешность

Проведение численных расчётов на компьютере неизбежно связано с погрешностью округления, иначе говоря, с вычислительной погрешностью. Округления возникают в силу ограниченности разрядной сетки компьютера при представлении в нем вещественных чисел. Правила, по которым производятся округления при ручном счёте, просты, и с ними можно познакомиться, например, в [1, c. 29–32]; [2, c. 24–25]. Округления в ЭВМ производятся путём отбрасывания цифр, не помещающихся в разрядную сетку. Следует отметить, что встречаются задачи, которые очень чувствительны к погрешностям исходных данных. Эта чувствительность может быть охарактеризована понятием устойчивости, которое входит как составная часть в понятие корректности. Сформулируем его.

Задача называется поставленной корректно, если для любых значений входных данных из некоторого класса выполняются следующие условия:

1) решение задачи существует и единственно в рассматриваемом классе решений;

2) решение устойчиво относительно входных данных, т.е. малые изменения во входных данных приводят к малому изменению решения.

Если нарушается одно из условий или сразу оба, то задача называется некорректно поставленной. В литературе представлено много примеров некорректно поставленных задач. Достаточно сослаться на пример Уилкинсона [4, c. 26–27] отыскания действительных корней многочлена:

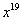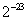Если незначительно изменить коэффициент при  (увеличить на ), то в результате вычислений вместо корней

получаются (при высокой точности расчётов) существенно иные корни. Этот пример иллюстрирует, что погрешность в исходных данных и погрешности округлений в процессе вычислений сильно искажают результат. Численные методы нецелесообразно применять к некорректно поставленным задачам. Эти задачи требуют особого рассмотрения, и для их решения разрабатываются свои методы.