1.7. Варианты заданий

Вариант №1

1. Найти сумму приближённых чисел , все знаки которых верны, и указать её абсолютную и относительную погрешности.

      2. Сторона квадрата равна

.

Вычислить площадь квадрата, округлив результат до верных знаков.

3. Вычислить значение функции при заданных значениях переменных. Указать абсолютную и относительную погрешности результата, считая все знаки в исходных данных верными:

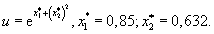
4. Определить количество верных значащих цифр в следующих числах:

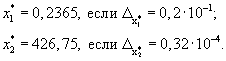
5. Найти допустимые абсолютные погрешности аргументов, позволяющих найти значение функции

с пятью верными знаками.

Вариант №2

1. Определить относительную погрешность чисел

,

если

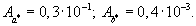
2. Определить количество верных значащих цифр в числах

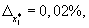
                                              если

                                               если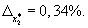

3. Найти частное двух чисел  (у делимого и делителя все знаки верные) и указать относительную погрешность результата.

4. Найти допустимое число верных значащих цифр свободного члена уравнения , чтобы получить корни с тремя верными знаками.

5. Вычислить значение функции

С какой абсолютной погрешностью следует задать , чтобы получить значение функции с тремя верными значащими цифрами.

Вариант №3

1. Определить количество верных значащих цифр в числах

 если

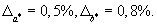
2. Определить абсолютную погрешность чисел

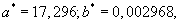 если

3. Найти произведение приближенных чисел

       – все знаки у сомножителей верные – и указать абсолютную и относительную погрешности результата.

4. С какой точностью должны быть измерены стороны  прямоугольника, чтобы его площадь можно было определить с абсолютной погрешностью 2 м²?

5. Определить абсолютную и относительную погрешности  функции , если .

Вариант №4

1. Приближённое значение величины . Зная, что 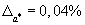, указать область неопределённости а.

      2. Вычислить выражение , считая, что все числа даны с верными знаками. Определить число верных значащих цифр результата.

3. Даны числа  и  с относительными погрешностями 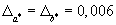. Определить величину относительной погрешности корня квадратного из их разности.

4. Найти абсолютную и относительную погрешности объёма шара , если диаметр шара .

5. Радиус основания цилиндра  высота. С какими абсолютными погрешностями надо определить  и , чтобы боковая поверхность цилиндра при ,  была вычислена с точностью 0,1 м²?

Вариант №5

1. Округлить сомнительные цифры числа, оставив верные знаки. Определить абсолютную погрешность результата:

                                    а)

                                    б) .

2. Вычислить абсолютную и относительную погрешности результата

, если

3. Найти допустимую абсолютную погрешность для , считая, что в исходном числе 1,244 все знаки верные.

4. С каким числом верных значащих цифр следует взять значение аргумента 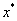, чтобы получить значение функции  с пятью верными значащими цифрами?

Принять .