2. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

Задача решения различного типа уравнений может быть записана в общем виде в терминах  функционального анализа (см. [1, с. 170–172]). Пусть даны два множества , элементы которых обозначаются соответственно  и могут быть произвольной природы, например числами, функциями и т. д. Будем говорить, что на множестве  задан оператор , если каждому элементу ставится в соответствие некоторый элемент

.

При этом  называют оригиналом, а  – изображением. Пусть далее задан элемент  и требуется найти элементы , для которых  является изображением. Данную задачу можно задать операторным уравнением

.

При этом предполагается, что решение задачи существует и единственно.

Особый интерес представляют уравнения с числовыми неизвестными и системы таких уравнений. Нетрудно видеть, что такие уравнения являются частным случаем операторных уравнений, когда множества  и  являются числовыми пространствами конечной размерности.

В этом случае уравнение можно записать в виде
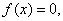	(2.1)
а систему уравнений в виде
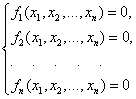или в векторной форме
,
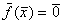где
, .
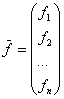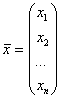