2.1. Общая теория алгебраических и трансцендентных уравнений

Рассмотрим уравнение вида (2.1), где  – некоторая функция, вообще говоря, комплекснозначная.

Совокупность значений переменной , при которых уравнение (2.1) обращается в тождество, называется решением этого уравнения, а каждое значение   из этой совокупности – корнем уравнения.

В зависимости от вида функции   уравнения вида (2.1) делят на алгебраические и трансцендентные.

Функцию  называют алгебраической, если для получения значения функции по данному  необходимо выполнить арифметические операции и возведение в степень с рациональным показателем (операцию извлечения корня степени 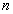можно представить как операцию возведения в степень с показателем ). Отметим, что алгебраическая функция называется рациональной относительно переменной , если над  производятся операции сложения, вычитания, умножения, деления и возведения в степень. В зависимости от степени  рациональная функция может быть либо целой рациональной, либо дробно–рациональной.

– пример целой рациональной функции;

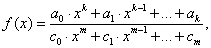
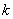где  – любые действительные числа,  – натуральное число или 0,  – натуральное число. Это пример дробно–рациональной функции.

К классу алгебраических функций также принадлежат и иррациональные  функции.

Функцию  называют иррациональной, если для получения её значения по данному  необходимо выполнить кроме арифметических действий (не обязательно всех), ещё и извлечение корня. При этом функция будет иррациональной, если аргумент находится под знаком корня.

Если в левую часть уравнения (2.1) входят только алгебраические функции, то уравнение называется алгебраическим.

Алгебраическое уравнение можно привести к виду

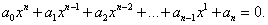(2.2)

Числа  – коэффициенты уравнения, причём это могут быть как вещественные, так и комплексные числа. Корни уравнения могут быть и вещественными, и комплексными. В данном пособии ограничимся рассмотрением случая, когда коэффициенты – вещественные числа. В случае, когда коэффициенты уравнения (2.2) – комплексные величины, можно обратиться к источникам (см.[2, с 517–523]).