2.4. Отделение действительных корней алгебраических уравнений

Пусть дано алгебраическое уравнение (2.1) или в развёрнутом виде (2.2) с действительными коэффициентами  .

В высшей алгебре доказывается ряд утверждений, позволяющих найти границы расположения корней уравнения (2.2) в комплексной области и отделить действительные корни.

Приведём без доказательства некоторые теоремы, позволяющие установить границы расположения корней уравнения (2.2) (см. [2, с. 452–458]).

Теорема 1. Если , , то все корни уравнения (2.2) расположены в кольце:

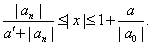(2.3)

Теорема 2. Если  – максимум модулей отрицательных коэффициентов уравнения,  и первый отрицательный коэффициент в последовательности  есть , то все положительные корни уравнения меньше

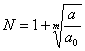
(если отрицательных коэффициентов нет, то нет и положительных корней).

Теорема 3. Если  и при  имеют место неравенства

то число  служит верхней границей положительных корней уравнения (2.2).

Теорема 4. Пусть заданы многочлены

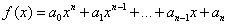	(2.4)

и  – верхние границы положительных корней соответственно многочленов  Тогда все положительные корни уравнения (2.2) лежат на отрезке , а все отрицательные корни –  на отрезке .

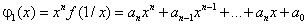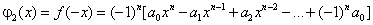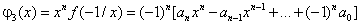Укажем далее несколько теорем, дающих возможность определить число действительных корней уравнения (2.2).

Теорема 5. (теорема Декарта). Число положительных корней уравнения (2.2) с учётом их кратности равно числу перемен знаков в последовательности коэффициентов  (при этом равные нулю коэффициенты не учитываются) или меньше этого числа на чётное число.

Заметим, что для определения количества отрицательных корней достаточно применить теорему Декарта к многочлену .

Отметим, что теорема Декарта, так же как и теорема Бюдана-Фурье (см. [2, с. 456]), не требует больших вычислений, но не всегда даёт точное количество действительных корней уравнения (2.2). Если уравнение (2.2) не имеет кратных корней на , то точное число действительных корней уравнения (2.2) на отрезке  даёт теорема Штурма.

Прежде чем её сформулировать, введём обозначения, предположив, что уравнение (2.2) не имеет кратных корней. Обозначим через  производную ; через  остаток от деления  на , взятый с обратным знаком; через  остаток от деления  на , взятый с обратным знаком, и так далее, до тех пор, пока не придём к постоянной. Полученную последовательность

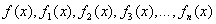(2.5)

назовём рядом Штурма.

Теорема 6 (теорема Штурма). Число действительных корней уравнения , расположенных на отрезке , равно разности между числом перемен знаков в последовательности (2.5) при  и числом перемен знаков в последовательности (2.5) при .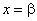

Заметим, что использование теоремы Штурма на практике связано с большой вычислительной работой при построении ряда Штурма.