2.5. Метод половинного деления (дихотомии)

Этот метод (см. [4, с. 118–119]) удобно применять для грубого отделения одного из корней уравнения (2.1) на некотором отрезке , если на нём корни не отделены.

Идея метода проста: пусть функция  непрерывна на  и . Для нахождения корня уравнения (2.1), принадлежащего , делим этот отрезок пополам. Если , то  есть корень уравнения. Если , то выбираем тот из отрезков  или , на концах которого  имеет противоположные знаки. Новый отрезок , полученный указанным способом, снова разделим пополам и выполним ту же процедуру. Продолжая этот процесс, либо на каком-то этапе получим точный корень уравнения (2.1), либо бесконечную последовательность вложенных друг в друга отрезков , , …, , … таких, что   причём

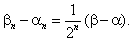(2.6)

Левые концы  образуют монотонно не убывающую ограниченную последовательность, а правые концы  – монотонно не возрастающую ограниченную последовательность. Из равенства (2.6) вытекает, что существует общий предел

.

Так как , то переходя в этом неравенстве к пределу при 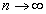, в силу непрерывности функции , получим .

Отсюда вытекает, что , т.е.  есть корень уравнения (2.1).

Очевидна оценка

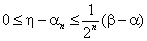(2.7)