2.6. Итерационные методы решения алгебраических и трансцендентных уравнений
2.6.1. Метод простой итерации
Отметим
прежде всего, что суть любого итерационного метода решения уравнения
(2.1) заключается в следующем. Пусть известен малый
промежуток ![]() , в
котором содержится единственный корень
, в
котором содержится единственный корень ![]() уравнения (2.1). Из достаточно малой
окрестности корня выбирается точка
уравнения (2.1). Из достаточно малой
окрестности корня выбирается точка ![]() – начальное приближение к корню уравнения и
строится последовательность значений
– начальное приближение к корню уравнения и
строится последовательность значений ![]() посредством рекуррентного соотношения
посредством рекуррентного соотношения
![]() ,
, ![]() .
.
При этом последовательность ![]() должна сходиться к корню
должна сходиться к корню ![]() , что обеспечивается
соответствующим выбором
, что обеспечивается
соответствующим выбором ![]() .
Простейшим из итерационных методов решения уравнения (2.1) является метод
простой итерации или метод последовательных приближений, применимый к широкому
классу уравнений вида (2.1). В этом методе (2.1) приводится к виду
.
Простейшим из итерационных методов решения уравнения (2.1) является метод
простой итерации или метод последовательных приближений, применимый к широкому
классу уравнений вида (2.1). В этом методе (2.1) приводится к виду
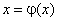 |
(2.8) |
Если ![]() (в прикладных задачах
(в прикладных задачах ![]() – конечный или бесконечный
отрезок числовой оси), а
– конечный или бесконечный
отрезок числовой оси), а ![]() принадлежит
принадлежит
![]() , то функцию
, то функцию ![]() можно рассматривать как оператор,
отображающий
можно рассматривать как оператор,
отображающий ![]() в
в ![]() . Решить уравнение (2.8) – значит
найти такие точки
. Решить уравнение (2.8) – значит
найти такие точки ![]() ,
которые при отображении оператором
,
которые при отображении оператором ![]() переходят в себя.
переходят в себя.
Как и в общем
подходе, в методе простой итерации на основе начального приближения ![]() , принадлежащего малой
окрестности корня уравнения (2.1), строят последовательность
, принадлежащего малой
окрестности корня уравнения (2.1), строят последовательность ![]() , по формуле
, по формуле
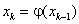 , ,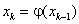 |
(2.9) |
Здесь функция ![]() не зависит от номера итерации
не зависит от номера итерации ![]() , и методы такого типа
называют стационарными.
, и методы такого типа
называют стационарными.
Геометрическая интерпретация метода простой итерации представлена на рис. 2.1. Отметим, что приведение уравнения (2.1) к виду (2.9) может быть сделано многими способами. Например, можно положить
![]() ,
,
где ![]() – произвольная непрерывная знакопостоянная
функция. Успех метода зависит от того, насколько удачно выбрана
– произвольная непрерывная знакопостоянная
функция. Успех метода зависит от того, насколько удачно выбрана ![]() .
.
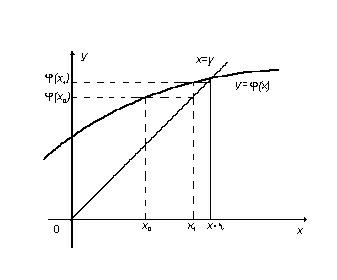
Рис. 2.1
Исследуем условия
сходимости метода (см. [5, с.142–143]). Пусть ![]() имеет непрерывную производную. Тогда
имеет непрерывную производную. Тогда
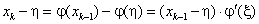 |
(2.10) |
Из (2.10) видно, что
если ![]() , то последовательность
, то последовательность
![]() убывает не
медленней членов геометрической прогрессии со знаменателем
убывает не
медленней членов геометрической прогрессии со знаменателем ![]() , и тогда последовательность
, и тогда последовательность ![]() сходится при любом не
нулевом приближении
сходится при любом не
нулевом приближении ![]() .
.
Если ![]() в некоторой окрестности
корня, то итерации не могут сходиться. Очевидно, что чем меньше
в некоторой окрестности
корня, то итерации не могут сходиться. Очевидно, что чем меньше ![]() , тем быстрее сходимость.
Сходимость будет особенно быстрой при
, тем быстрее сходимость.
Сходимость будет особенно быстрой при ![]() .
.
Если функция ![]() удовлетворяет условию
Липшица в круге
удовлетворяет условию
Липшица в круге ![]() ,
т.е.
,
т.е.
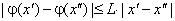 |
(2.11) |