Теорема. Каково бы ни было , последовательность  сходится к корню  уравнения (2.1), если только функция в круге  удовлетворяет условию Липшица с константой , причём скорость сходимости определяется неравенством

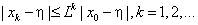(2.12)

Обсудим вопрос, когда прекращать итерации на практике. Как видно из (2.10), если , итерации попеременно оказываются то справа, то слева от корня. Тогда корень   будет заключён в интервале , что является надёжной, но несколько грубой оценкой. Однако она не применима, если  и итерации сходятся к корню монотонно, т.е. с одной стороны.

В малой окрестности корня итерации сходятся примерно так же, как геометрическая прогрессия со знаменателем

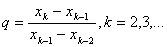(2.13)

Итерации можно прекратить, если выполняется условие (см. [5, с. 142]):

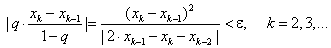(2.14)

Здесь  – точность вычислений.

Из (2.10) следует, что метод простой итерации является методом первого порядка точности, поскольку  пропорционально .

2.6.2. Метод Ньютона

Этот метод является ещё одним классическим методом решения уравнений вида (2.1). Иначе его называют методом касательных или методом линеаризации (см. [5, с. 143–145]).

Предположим, что на  содержится единственный корень  уравнения (2.1) и функция  дважды непрерывно дифференцируема, причём  и  не равны нулю на . Приведём уравнение (2.1) к виду (2.8). Полагаем при этом

,

т.е. будем рассматривать метод Ньютона как частный случай метода простой итерации. Выберем произвольную точку  из малой окрестности корня  и так, чтобы выполнялось условие

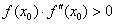(2.15)

и построим итерационную последовательность по формуле

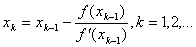(2.16)

Последовательность (2.16) будет сходиться, так как

 и, следовательно, .

Последнее означает, что если  выбрано из достаточно малой окрестности , то .

При произвольном  итерации будут сходиться, если всюду

.

Геометрически формула (2.16) означает, что на каждой итерации график функции  заменяется касательной к нему (рис. 2.2).

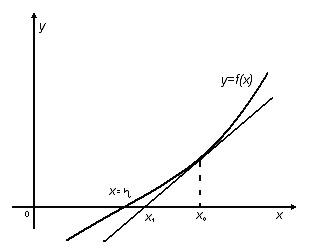
Рис. 2.2

Отметим, что условие (2.15) даёт монотонную сходимость итерационного процесса к корню  с той стороны, с какой выбирается .

Оценим скорость сходимости метода Ньютона (см. [5, с.144]). Используя (2.10), имеем:

.

Разложим  по формуле Тейлора в точке  и учтём, что . Получим

,

или

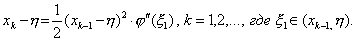(2.17)

Из формулы (2.17) видно, что погрешность очередного  приближения примерно равна квадрату погрешности предыдущего приближения. Поэтому метод Ньютона является методом второго порядка точности. Он обеспечивает более быструю сходимость по сравнению с методом простой итерации. Если известны хорошие начальные приближения для корней произвольной дифференцируемой функции, то для их уточнения чаще всего применяют метод Ньютона.