2.6.3. Другие итерационные методы

Вычислительная работа метода Ньютона связана с нахождением  и . Её можно уменьшить, если заменить, например, производную  первой разделённой разностью по двум точкам  и или, что то же, заменить касательную секущей, т.е. положить

.

Тогда формула (2.16) перейдёт в следующую формулу:

или

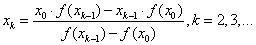(2.18)

Чтобы строить итерационную последовательность по формуле (2.18), нужно задать два начальных приближения  и . Итерационные процессы, где для вычислений очередного приближения требуется знание двух предыдущих, называют двухшаговыми.

Как показано в  [2, с. 465–466], в методе секущих

.

Если  взято достаточно близко к корню , то  – малое число. Тогда существует такая окрестность корня , в которой

.

           Если  также принадлежит этой окрестности, то итерационная последовательность будет сходиться к корню . Отметим, что сходимость итераций может быть немонотонной как вдали от корня, так и в малой окрестности корня (см. [5, с. 145]). Погрешность  в методе секущих убывает по закону, близкому к убыванию в методе Ньютона, но с несколько меньшей скоростью стремления к нулю.

Заметим, что в формуле (2.18) в знаменателе стоит разность значений функции.

Вблизи корня значения функции малы и близки. Возникает потеря значащих цифр, что ограничивает точность получаемого значения корня. Метод секущих является итерационным методом первого порядка точности.

Можно получить нестационарный метод нахождения действительных корней уравнения (2.1), комбинируя метод Ньютона и метод секущих (см. [2, с. 467–470]).

Пусть на отрезке  содержится единственный корень уравнения (2.1) и  не меняют знаков на . Начальные приближения  и  получаем по формулам:

, ,

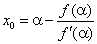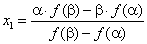(2.19)

если . Если же , то  и  задаём по формулам:

,.

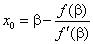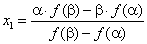(2.20)

Остальные приближения вычисляем,пользуясь формулами:

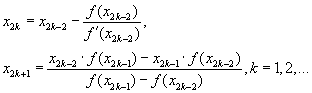(2.21)

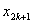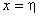Последовательные приближения  и  лежат всегда по разные стороны от корня . В процессе вычислений можно следить за точностью результатов. Комбинированный метод сходится значительно быстрее метода секущих.

Замечание. Почти все итерационные методы решения уравнения (2.1) обладают тем свойством, что в них не накапливаются ошибки вычислений. Если в процессе счёта допущена ошибка, то она не отразится на точности окончательного результата, а лишь на числе итераций, так как этот процесс самоисправляющийся.

В завершение рассмотрения итерационных методов решения нелинейных уравнений приведем примеры блок-схем некоторых из них, что, несомненно, облегчит понимание логической основы алгоритмов методов

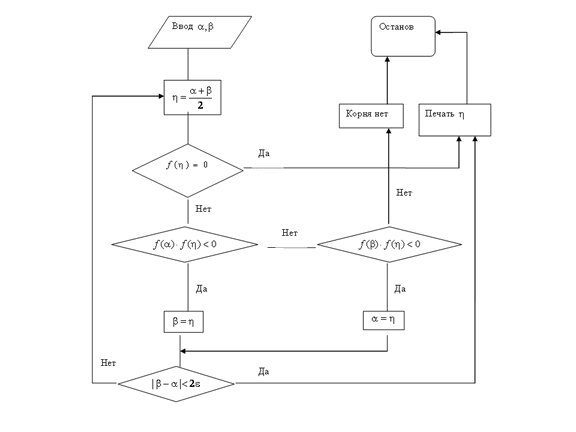
Блок-схема метода дихотомии

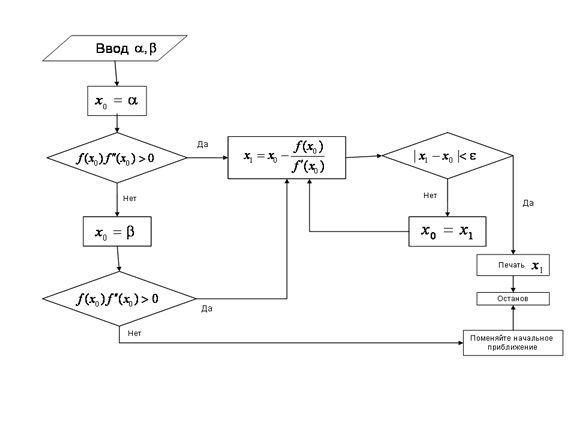
Блок-схема метода Ньютона