2.7.Задания

1. Отделить корни уравнения .

2. Уточнить с точностью 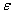корни уравнения одним из итерационных методов.

2.7.1. Решение одного варианта задания

Проиллюстрируем применение вышеизложенной теории на двух примерах.

В качестве итерационного метода уточнения корней рассмотрим метод Ньютона.

ПРИМЕР 1

Отделить корни алгебраического уравнения  одним из аналитических методов и затем уточнить их методом касательных с точностью .

1. Воспользуемся теоремой 4.

Обозначим:

,

,

,

Тогда

,

,

.

По теореме 4 корни принадлежат одному из промежутков . В данном примере корни уравнения могут лежать на интервалах .

1.      Для отделения корней используем теорему Штурма.

Ряд Штурма будет выглядеть следующим образом:

,

,

,

.

Поместим в табл. 2.1 знаки функций из ряда Штурма на промежутках

Таблица 2.1
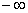
x –1 –0,4 0,5 1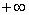
– – + + + +
+ + + + + +
– – – – – +
– – – – – –
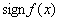
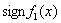
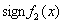
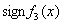
Число перемен знаков 2 2 1 1 1 1

Из таблицы видно, что есть один действительный корень данного уравнения , и он находится на промежутке .

Корень уточним методом касательных. В качестве начального значения берём , т.к. . Получим:

итерация № 0 – ,

итерация № 1 – ,

итерация № 2 – ,

итерация № 3 – ;

число итераций – 3.

Корень , .

ПРИМЕР 2

С помощью графического метода отделить корни трансцендентного уравнения  и уточнить их методом Ньютона с точностью .

1. Запишем уравнение в виде , где

.

Графики  представлены на рис. 2.3. Из рис. 2.3 видно, что первый корень , а второй корень .

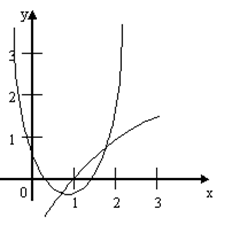
Рис. 2.3

2. Уточним корни методом касательных. Имеем

.

Формула метода Ньютона имеет вид

,            .

Т.к. , то для первого корня, следовательно, . Результаты расчетов для первого и второго корня помещены в табл. 2.2, 2.3.

Таблица 2.2
k 0 1 2 3 4 5 6 7
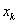
0,1 0,351067 0,668912 0,836598 0,872805 0,874392 0,874395 0,874395
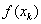
–2,962385 –1,317894 –0,361721 –0,055112 –0,002221 –0,000004 0,000000  
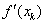
11,8 4,146330 2,157199 1,512122 1,400120 1,394868 1,394858  

Таблица 2.3
k 0 1 2 3 4
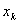
2 1,8954315 1,8856545 1,8855667 1,8855667
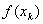
–0,1568528 –0,01235106 –0,0001089 –0,00000001  
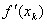
–1,5 –1,2632786 –1,2409892 –1,2407889  

Для второго корня принято, что .