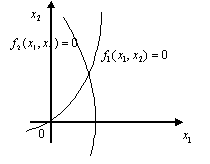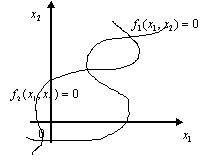3. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Задача решения систем нелинейных уравнений часто встречается на практике. Достаточно вспомнить, что решение нелинейных краевых задач (как для обыкновенных дифференциальных уравнений, так и для уравнений с частными производными) методом конечных разностей, а также минимизация функций многих переменных численными методами приводят к нелинейным системам уравнений (см., например, [1, с.438–444]).
В настоящем разделе рассмотрим проблему численного решения систем нелинейных уравнений и покажем, как описанные в [2] методы переносятся на этот случай.
Пусть требуется найти приближенное решение системы нелинейных уравнений:
 |
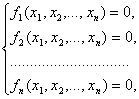(3.1) |
– заданные функции 
переменных 
. Здесь под решением
понимается такой набор вещественных чисел 
, что при подстановке их в (3.1) получаются
тождества.
Систему (3.1) можно представить в векторном виде:
,
где
 ,  . |
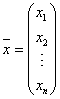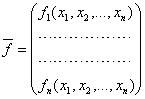(3.2) |
Как видно из (3.1),
при 
имеет место
рассмотренный в гл. 2 случай одного нелинейного уравнения.
При численном решении
системы (3.1) неизбежно возникает вопрос о существовании решения и его
единственности. В общем случае ответить на этот вопрос очень сложно. В случае
системы двух нелинейных уравнений (
):
 |
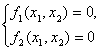(3.3) |
ответ на вопрос о существовании решения можно, в принципе,
найти геометрическим способом. Для этого на плоскости 
нужно изобразить графики функций
и
. Точки пересечения графиков и дадут
множество решений системы (3.3).
Несколько возможных ситуаций в
случае представлено
на рис.3.1.
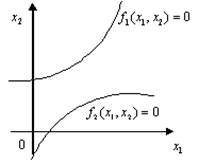
Случай :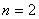
|
|
|
|
|
Единственное решение |
Несколько решений |
Нет решений |
Рис. 3.1
В дальнейшем предполагается, что система нелинейных уравнений (3.1) имеет интересующее нас вещественное решение
,
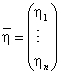хотя оно может быть и не единственным.
Перейдём теперь к описанию методов приближенного решения систем вида (3.1). Наиболее распространены на практике следующие итерационные методы: метод простой итерации (см. [1, c. 317–323]; [3, c. 179–185]; [4, c.164–165]); метод Ньютона (см. [1, c. 323–329]; [3, c. 189–190]; [4, c.165–168]); метод Зейделя (см. [1, c. 320–321]; [7, c. 192–193]); методы секущих или, как их называют иначе, дискретные варианты метода Ньютона (см. [10, c.62–66]); метод Гаусса-Зейделя (см. [10, c. 55–58]). Известны и другие методы, детальное описание которых можно найти в пособиях [1, 4, 5, 10].
Среди итерационных методов наиболее легко реализуется метод простой итерации.