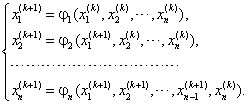3.1. Метод простой итерации
Дана система ![]() нелинейных уравнений (3.1)
или в векторном виде (3.2). Для применения метода простой итерации система (3.1)
или (3.2) приводится к виду
нелинейных уравнений (3.1)
или в векторном виде (3.2). Для применения метода простой итерации система (3.1)
или (3.2) приводится к виду
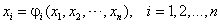 |
(3.4) |
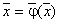 |
(3.5) |
Система нелинейных
уравнений (3.5) записана для элементов ![]() -мерного пространства
-мерного пространства ![]() , причём, элемент
, причём, элемент ![]() этого пространства служит
для изображения значений аргументов
этого пространства служит
для изображения значений аргументов ![]() функций
функций ![]() , а элемент
, а элемент ![]() – для изображения соответствующих значений
– для изображения соответствующих значений ![]() . Зависимость вида (3.5)
можно рассматривать как отображение пространства
. Зависимость вида (3.5)
можно рассматривать как отображение пространства ![]() в себя.
в себя.
Если обозначить
точное решение (3.5) через ![]() и предположить, что за начальное приближение
к точному решению выбрано
и предположить, что за начальное приближение
к точному решению выбрано ![]() , то дальнейшие приближения строятся по
формуле
, то дальнейшие приближения строятся по
формуле
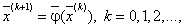 |
(3.6) |
где ![]() –
номер приближения или итерации. Итерационный процесс продолжается до тех пор,
пока не выполняются неравенства
–
номер приближения или итерации. Итерационный процесс продолжается до тех пор,
пока не выполняются неравенства ![]() - принятая точность вычислений.
- принятая точность вычислений.
Будем предполагать,
что функция ![]() достаточно
гладкая в окрестности точки
достаточно
гладкая в окрестности точки ![]() . Обозначим через
. Обозначим через ![]() – вектор погрешности. Если
– вектор погрешности. Если ![]() близко к
близко к ![]() , то из (3.6) будет
следовать, что
, то из (3.6) будет
следовать, что
![]() .
.
Или отсюда имеем
![]() .
.
Если предположить, что матрица
Якоби ![]() невырождена
при
невырождена
при ![]() , то,
пренебрегая величиной
, то,
пренебрегая величиной ![]() ,
получим приближенную формулу, связывающую значения вектора погрешности на двух
шагах итерации –
,
получим приближенную формулу, связывающую значения вектора погрешности на двух
шагах итерации – ![]() и
и
![]() , т. е.
, т. е.
![]() .
.
Из последней формулы, очевидно, имеем
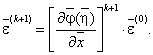
Для сходимости метода простой
итерации при любом ![]() необходимо,
чтобы
необходимо,
чтобы
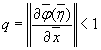 ,
,
где под ![]() понимается одна из норм матрицы
(см. [1, с.255–257]). Скорость сходимости метода зависит от величины
понимается одна из норм матрицы
(см. [1, с.255–257]). Скорость сходимости метода зависит от величины ![]() и, если
и, если ![]() близко к 1, то скорость
сходимости невысокая (см. [10, с.54–55]).
близко к 1, то скорость
сходимости невысокая (см. [10, с.54–55]).
Обсудим, как от
системы (3.2) перейти к (3.5) . Рекомендуется функцию ![]() из (3.5) искать в виде
из (3.5) искать в виде
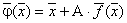 |
(3.7) |
Здесь
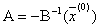 ,
,
где 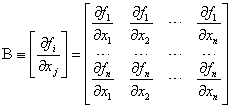 - матрица Якоби - матрица Якоби |
(3.8) |
Будем предполагать, что матрица ![]() – неособенная. Подставив
выражение
– неособенная. Подставив
выражение ![]() из
формулы (3.7) в (3.5), запишем следующую итерационную формулу:
из
формулы (3.7) в (3.5), запишем следующую итерационную формулу:
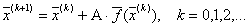 |
(3.9) |
Приведём запись этой формулы для соответствующих компонент
вектора ![]() :
:
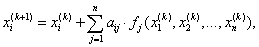 |
(3.10) |
![]() – элементы
матрицы
– элементы
матрицы ![]() .
.
Остановимся на вопросе о сходимости метода простой
итерации для случая системы ![]() нелинейных уравнений. Будем предполагать, что
нелинейных уравнений. Будем предполагать, что
![]() – метрическое
пространство.
– метрическое
пространство.
Говорят, что отображение (3.5) является сжимающим
(см. [1, c.319]), если при некотором ![]() отображение
отображение ![]() удовлетворяет условию
удовлетворяет условию
![]()
при всех ![]() – расстояние в
– расстояние в ![]() (см. [3, с. 179]).
(см. [3, с. 179]).
Теорема. Если отображение ![]() сжимающее, то уравнение (3.5)
имеет решение
сжимающее, то уравнение (3.5)
имеет решение ![]() и
и
![]() .
.
Здесь ![]() .
.
Доказательство теоремы можно найти в [1, c.319–320].
Замечание. Вместо метода простой итерации иногда более удобно применять процесс Зейделя: