3.2. Метод Ньютона
Метод Ньютона является эффективным методом
повышения точности решения системы нелинейных уравнений (3.1) в тех случаях,
когда известно достаточно хорошее приближение ![]() ,
, ![]() , к точному решению
, к точному решению ![]() .
.
Идея метода состоит в следующем: в окрестности
приближения ![]() заменим
задачу (3.1) вспомогательной линейной задачей. Обозначим
заменим
задачу (3.1) вспомогательной линейной задачей. Обозначим
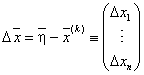 ,
, ![]()
и представим (3.1) в виде
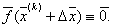 |
(3.14) |
Предположим, что функции ![]() , дважды непрерывно дифференцируемы в области
, дважды непрерывно дифференцируемы в области ![]() , содержащей точку
, содержащей точку ![]() , а величина
, а величина ![]() мала. Тогда,
воспользовавшись формулой Тейлора, получим приближенное равенство:
мала. Тогда,
воспользовавшись формулой Тейлора, получим приближенное равенство:
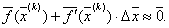 |
(3.15) |
В формуле (3.15) под ![]() понимается матрица Якоби
понимается матрица Якоби 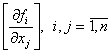 , или в развёрнутом виде:
, или в развёрнутом виде:
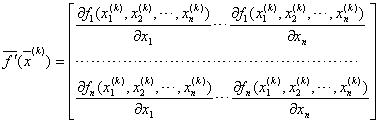 .
.
Формула (3.15) представляет собой систему линейных
алгебраических уравнений относительно ![]() , причем все её коэффициенты выражаются через
, причем все её коэффициенты выражаются через ![]() ,
, ![]() . Решив эту систему любым известным
методом, например по правилу Крамера, методом исключения Гаусса (см. [1, c.257–265]), полагаем
. Решив эту систему любым известным
методом, например по правилу Крамера, методом исключения Гаусса (см. [1, c.257–265]), полагаем
![]() .
.
Если использовать формулы (3.18), то на каждой
итерации требуется находить ![]() Таким образом, фактическая реализация метода
Ньютона проводится в два этапа:
Таким образом, фактическая реализация метода
Ньютона проводится в два этапа:
1) решаем систему линейных алгебраических уравнений
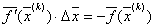 |
(3.16) |
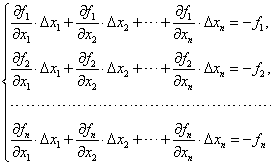 |
Значения функций ![]() и их производных вычисляем
в известной точке
и их производных вычисляем
в известной точке ![]() .
При этом предполагаем, что
.
При этом предполагаем, что ![]() ;
;
2) полагаем
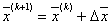 |
(3.17) |
![]() и переходим к п. 1.
и переходим к п. 1.
Счёт прекращаем, когда все приращения ![]() неизвестных становятся малыми по
абсолютной величине, а именно:
неизвестных становятся малыми по
абсолютной величине, а именно:
![]() ,
,
где 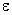 –
заданная точность вычислений.
–
заданная точность вычислений.
Если матрицы Якоби ![]() являются невырожденными, то из (3.15)
получим ещё одну запись итерационного процесса:
являются невырожденными, то из (3.15)
получим ещё одну запись итерационного процесса:
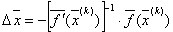 |
(3.18) |
![]() .
.
Формула (3.18) есть обобщение
метода Ньютона для одного уравнения (см. [2, c.12–13])
на случай ![]() уравнений.
Из приведённых здесь обобщений метода Ньютона на случай
уравнений.
Из приведённых здесь обобщений метода Ньютона на случай ![]() уравнений алгоритм (3.16) – (3.17)
является наиболее последовательным и обладает следующими достоинствами:
уравнений алгоритм (3.16) – (3.17)
является наиболее последовательным и обладает следующими достоинствами:
1. Сходимостью итераций к точному решению при условиях, которые даёт следующая теорема.