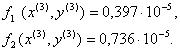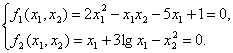
3.3. Лабораторные задания

Задание.        

1. Получить начальное приближение к решению системы двух нелинейных уравнений графическим способом.
2. Уточнить решение системы до тысячных долей, используя итерационные методы.

Пример решения варианта задания

1. Методом простой итерации. Рассмотрим пример из [8, c.150].

Дана система уравнений

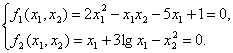
Определить положительные корни этой системы с тремя значащими цифрами.

Решение

1. Определим начальное приближение к корням системы графическим способом. Из рис. 3.2 видно, что в качестве начального приближения можно взять .

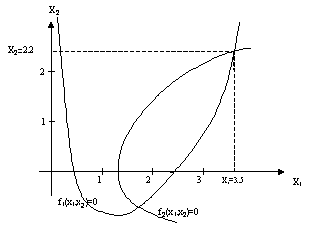
Рис. 3.2

Чтобы применить метод простой итерации, запишем данную систему в виде:

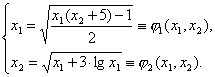
Итерационный процесс строится по формулам:

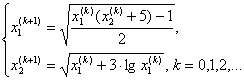
Проверим, выполняется ли достаточный признак сходимости метода простой итерации.

Определим

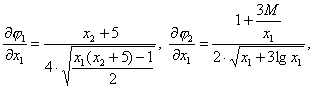
где

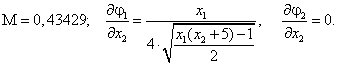
Если рассматривать окрестность

, то получим, что

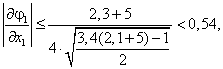
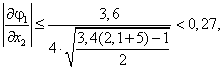
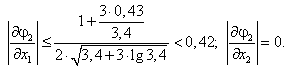
Отсюда находим, что

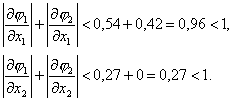
Итак, если последовательные приближения  не будут выходить за пределы области G (это легко обнаружить в процессе вычислений), то итерационный процесс сходится.

2. Результаты вычислений приведём в виде табл. 3.2.

Таблица 3.2

K
0 1 2 3 4 5 6	3,5 3,479 3,481 3,484 3,486 3,484 3,487	2,2 2,259 2,260 2,261 2,261 2,262 2,262

В качестве корней можно взять .

2. Методом Ньютона. Проиллюстрируем выполнение задания на примере решения системы

1. Получим начальное приближение к решению данной системы. Для этого построим графики функций

и

в плоскости переменных . Они будут иметь вид, изображенный на рис. 3.3

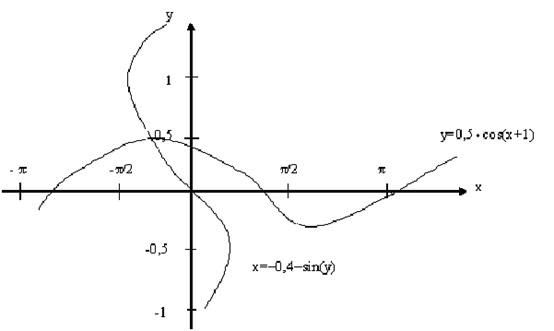
Рис. 3.3

Из графиков следует, что система имеет единственное решение, и за начальное приближение к решению можно принять .

2. Уточним начальное приближение по методу Ньютона с точностью .

Исходная система имеет вид

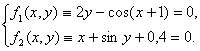
Согласно методу Ньютона при заданных  последующие приближения к решению находятся по итерационным формулам (3.22). Для проведения расчетов по ним получим вид . Имеем

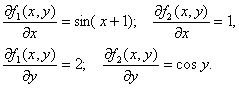
Тогда

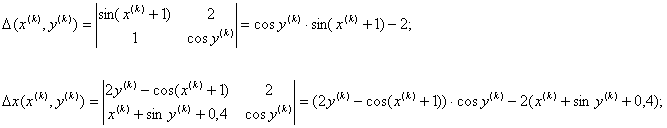
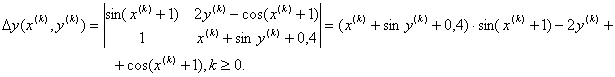
Получаем , т.е. матрица Якоби невырождена. Уточнение решения заданной системы проведём по формулам:

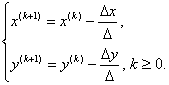
При  через  итерации с точностью  получаем решение:

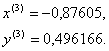
При этом имеем