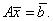
4. ТОЧНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)

4.1. Общие замечания

К основным проблемам линейной алгебры относятся следующие: решение систем линейных уравнений, вычисление определителей, нахождение элементов обратной матрицы, вычисление собственных значений и собственных векторов матриц. В данном разделе рассмотрим первую задачу, решая вместе с ней вторую и третью.

Задача решения систем линейных алгебраических уравнений (СЛАУ) часто встречается в приложениях. К решению систем линейных уравнений приводятся краевые задачи для обыкновенных дифференциальных уравнений и уравнений с частными производными, если их решать разностными методами (см. [1, с. 357–570]; [2, с. 193–243]; [3, с. 205–291]; [4, с. 237–451]), задача интерполяции и построение кубического сплайна (см. [1, с. 194–203]; [2, с. 63–68]; [5, с. 21–76]; [6, с. 46–149]), численное решение интегральных уравнений (см. [1, с. 571–579]; [3, с. 292–299]; [4, с. 452–460]) и др.

Запишем систему линейных алгебраических уравнений в виде

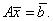(4.1)

Здесь  – квадратная матрица порядка ;

 – вектор-столбец неизвестных и вектор-столбец правых частей соответственно. При этом , где  – вещественное линейное -мерное векторное пространство.

Систему (4.1) можно записать в развернутом виде:

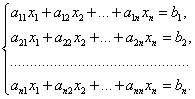(4.2)

Необходимым и достаточным условием существования единственного решения

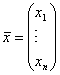
системы (4.1) или (4.2) является . Если , то система (4.1) или не имеет решения, или имеет бесчисленное множество решений.

Проиллюстрируем эти случаи на примере системы ():

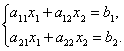(4.3)

Каждое уравнение системы (4.3) задает на плоскости  прямую. Решением системы (4.3) являются координаты точки пересечения заданных прямых.

В случае системы (4.3) возможны следующие три ситуации:

а)       Тогда
и прямые пересекаются в единственной точке (рис. 4.1, а).

б) 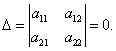      Тогда
и наклоны прямых равны. Прямые либо параллельны, либо совпадают (рис. 4.1, б).

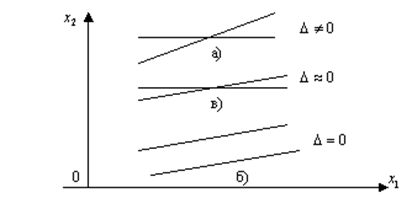
Рис. 4.1

в)      
В этом случае прямые почти параллельны и координаты точки их пересечения чувствительны к ошибкам округлений. Другими словами, малые погрешности округлений могут привести к существенным изменениям в решении. Такие системы уравнений принято называть плохо обусловленными (см. [4, c. 126–127]).

Отметим, что близость  к нулю является необходимым, но не достаточным условием для плохой обусловленности системы (4.3).

В теоретических исследованиях вводится число обусловленности матрицы, которое основывается на понятии нормы матрицы.