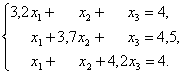
4.11. Решение варианта задания

Пример 1. Методом квадратного корня решить систему уравнений:

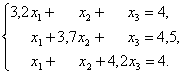(4.47)

Решение. Все вычисления помещаем в табл. 4.1 (см. [9, с. 68]).

Прямой ход

1. В первый раздел таблицы записываем коэффициенты системы и свободные члены.
2. Суммируем элементы по каждой строке и получаем величины

которые записываем в последнем столбце табл. 4.1 (раздел I).

       3. Находим  с помощью формул:

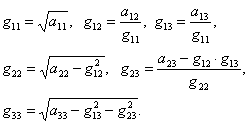(4.48)

Последовательно получаем:

4. По формулам, аналогичным (4.48), вычисляем:

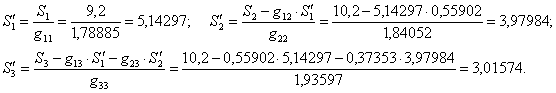
Обратный ход

5. По формулам (4.45) находим :

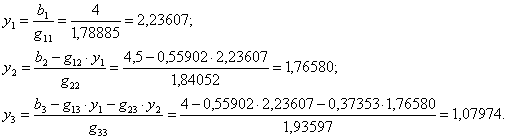
Полученные  помещаем в табл. 4.1 в раздел II, где записаны  и .

6. Проводим контроль вычислений. Для этого находим суммы:

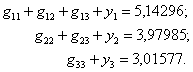
Сравниваем их с  Видим, что результаты совпадают до

Переходим к последнему этапу.

7. По формулам (4.46) находим :

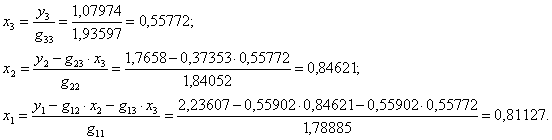
Полученные значения  записываем в раздел III табл. 4.1.

8. Найденные значения  подставляем в исходную систему. Получаем:

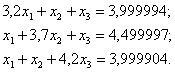
Сравнение полученных правых частей с  показывает, что отличие наблюдается в пятом разряде после запятой, что вполне допустимо.

Таблица 4.1

Пример 2. Решить систему линейных алгебраических уравнений, используя метод Гаусса с выбором главного элемента:

,

где

 – симметрическая матрица.

Решение.

Будем использовать табл. 4.2:

Таблица 4.2

Выпишем треугольную матрицу  системы (4.23), которая получается в результате применения схемы Гаусса с выбором главного элемента:

Решая эту систему “снизу вверх”, последовательно определим:

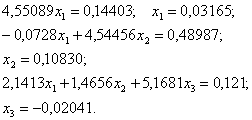
Для проверки правильности обратного хода схемы вычислим соответствующие :

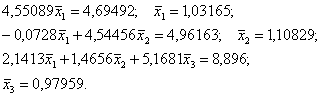
Сравнивая  и , видим, что:

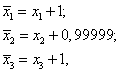
т.е.  отличаются от  на 1, а  и  на 0,99999.

Это вполне допустимая точность вычислений.

Замечание. Пояснения к табл. 4.2, приведенной выше, можно посмотреть в [9, с. 48], а смысл обозначений, используемых в табл. 4.2, – в разделе 4 данной главы.