4.2. Некоторые сведения о нормах векторов и матриц

Напомним, что решение системы (4.1) рассматриваем в вещественном линейном  -мерном векторном пространстве . При этом матрицу  отождествляем с линейным оператором . В пространстве  можно ввести норму вектора несколькими способами (см. [5, с. 80–87]):

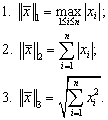(4.4)

Нетрудно убедиться, что эти нормы удовлетворяют трем аксиомам норм (см. [5, с. 83]).

При решении задач линейной алгебры матрицы и векторы рассматриваются одновременно. Поэтому норму матрицы  определяют так, чтобы она была согласованной с нормой вектора  (см. [5, c. 84]).

Определение 1. Говорят, что норма матрицы  согласована с нормой вектора , если для любого вектора  выполняется неравенство

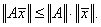(4.5)

При получении оценок точности  решения среди всех согласованных норм матрицы выбирают наименьшую

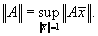(4.6)

Такая норма матрицы называется нормой, подчиненной норме вектора.

Справедливы следующие утверждения (см. [5, c. 85–86]):

1) если норма вектора

,

то подчиненная ей норма матрицы есть

2) если норма вектора

то подчиненная ей норма матрицы есть

3) если норма вектора

то подчиненная ей норма матрицы есть

где  – наибольшее собственное значение матрицы .

Определение 2. Число λ называется собственным значением матрицы , если существует такой ненулевой вектор , что справедливо

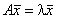(4.7)

Из (4.7) следует, что

С другой стороны, по определению нормы матрицы имеем

Тогда

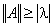(4.8)

и неравенство (4.8) означает, что любая норма матрицы больше либо равна модулю произвольного своего собственного значения, в том числе

Определение 3. Число

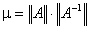(4.9)

называется числом обусловленности матрицы  (см. [4, с. 127]).

При любой норме матрицы  числоμ, и чем оно больше, тем хуже обусловленность системы (4.1). Как следует из [4, с. 127], если , то это уже означает плохую обусловленность.

Заметим, что вычисление μ связано с нахождением обратной матрицы, а это не всегда легко сделать.

Пример (плохо обусловленная система).

Пусть требуется решить систему линейных уравнений

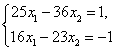(4.10)

или

, где

Решение.

Так как

то решение системы существует и единственно. Непосредственной подстановкой в систему можно убедиться, что

Определим число обусловленности матрицы . Имеем по определению 3

.

В нашем примере обратную матрицу  найти просто:

В качестве нормы матрицы выберем

Тогда

и число обусловленности матрицы

.

Следовательно, система (4.10) является плохо обусловленной.