4.3. Классификация методов решения систем линейных алгебраических уравнений

Если , то из (4.1) можно найти

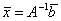(4.13)

где обратная матрица  может быть вычислена по правилу:

,

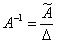(4.14)

Здесь  – алгебраические дополнения к элементам  матрицы .

Кроме указанного метода решения систем вида (4.1), существует известное правило Крамера (см. [7, с. 268–272]), согласно которому неизвестные

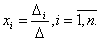(4.15)

Здесь  – определитель, получающийся из  заменой i-го столбца столбцом свободных членов

Отметим, что решение системы (4.1) по правилу Крамера или по формулам (4.13) – (4.15) практически невыгодно, т.к. требует большого объема вычислений. Так, например, использование правила Крамера приводит к вычислению -го определителя, а непосредственное развертывание определителя -го порядка требует примерно  арифметических операций (см. [4, с. 130–131]).

Если матрица исходной системы (4.1) имеет диагональный или треугольный вид, то решение системы (4.1) или (4.2) находится легко.

В самом деле, пусть

.

Тогда, если  имеем

В случае, когда матрица  является нижней треугольной, система (4.2) принимает вид

Отсюда, если , последовательно находятся  по формулам:

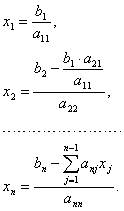
Подобные формулы нахождения  получаются и в случае, когда  есть верхняя треугольная матрица.