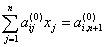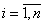
4.4. Метод Гаусса последовательного исключения неизвестных

Запишем систему линейных алгебраических уравнений (4.1) в виде

,

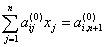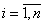(4.16)

где  – элементы матрицы ,  – компоненты вектор-столбца .

Для решения системы (4.16) воспользуемся методом Гаусса последовательного исключения неизвестных (схема единственного деления).

Метод Гаусса последовательного исключения неизвестных можно изложить с помощью -теоремы. Используя разложение матрицы  исходной системы на произведение левой и правой треугольных матриц, решение исходной системы сводят к последовательному решению двух систем с треугольными матрицами. Подробное изложение алгоритма такого подхода можно найти в [1, с. 257–261].

В настоящей работе остановимся на другом подходе реализации метода Гаусса. Суть его в том, что последовательно исключаются неизвестные  и задача сводится к решению системы с треугольной матрицей, эквивалентной исходной системе. Рассмотрим алгоритм данного подхода для случая  (см. [1, с. 257–258]; [2, с. 139–143] и др.).

Если ведущий элемент , то, поделив коэффициенты первого уравнения системы (4.16) на этот коэффициент, преобразуем уравнение к виду

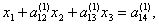(4.17)

где

Далее умножим каждый член (4.17) на , и вычтем его из соответствующего -го уравнения системы (4.16). В результате получится система из двух уравнений, в которой отсутствует :

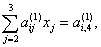(4.18)

где .

Если в полученной системе уравнений (4.18) коэффициент  при  ( – ведущий элемент) не равен 0, то преобразуем это уравнение по правилу, указанному выше: делим коэффициенты при неизвестных на . В результате получим

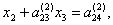(4.19)

где

Умножим левую и правую части (4.19) на , и вычтем из -го уравнения системы (4.18). В результате получим одно уравнение с одним неизвестным :

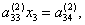(4.20)

где .

Если  то из уравнения (4.20) определяется неизвестная величина

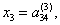(4.21)

где

В результате проведенных преобразований получилась система линейных алгебраических уравнений с треугольной матрицей, состоящая из уравнений (4.17), (4.19), (4.21). Матрица коэффициентов при неизвестных  в уравнениях этой системы имеет следующий вид:

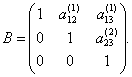(4.22)

Указанная система в векторной форме записывается так:

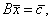(4.23)

где  имеет вид (4.22),

Отметим, что переход от исходной системы уравнений (4.16) к системе (4.23) с треугольной матрицей называется прямым ходом схемы Гаусса.

Обратный ход схемы Гаусса состоит в определении компонент вектора решения . Для этого надо решить систему (4.23) с треугольной матрицей. Сначала определяется неизвестное  по формуле (4.21), затем находят .

Соответствующие расчетные формулы для определения  и  определяем из уравнений (4.19) и (4.17) соответственно:

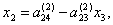(4.24)

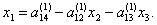(4.25)