4.7. Метод прогонки

Метод прогонки является частным случаем метода Гаусса и применяется к системам с трех-пятидиагональной матрицей (см. [2, с. 161–166]). Такие системы часто встречаются при численном решении краевых задач для дифференциальных уравнений второго порядка, при моделировании некоторых инженерных задач. Примером подобной системы является система, которая получается при построении кубического сплайна (см. [1, с. 194–203]).

Если при решении таких систем применять метод Гаусса, то расчет можно организовать таким образом, чтобы не включать нулевые элементы матрицы. Этим самым экономится требуемая память и уменьшается объем вычислений. Указанное ускорение вычислений допускают системы линейных алгебраических уравнений с ленточными, блочными,квазитреугольными, почти треугольными и другими матрицами (см. [4, с. 132–133]).

Запишем систему в каноническом виде (см. [4, с.133])

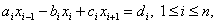(4.28)

где

В векторной форме она запишется так:

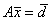(4.29)

где

  .

Предполагается, что

Метод прогонки состоит из двух этапов: прямой прогонки и обратной прогонки. На первом этапе определяются прогоночные коэффициенты, а на втором – находят неизвестные .

Если в системе (4.29) выразить из первого уравнения  через , а затем подставить выражение  во второе уравнение, связывающее , то получим уравнение относительно  и :

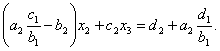(4.30)

Из этого уравнения можно получить выражение  через . Далее, рассуждая аналогично, подставим в -е уравнение системы (4.29) выражение  через , полученное из   -го уравнения, и затем выразим  через . В этом выражении в правой части при  будут стоять некоторый коэффициент и свободный член.

Если определить неизвестную , то из формулы, связывающей  и , легко найти . Зная , определяем  и т.д., пока не найдем значение .

В силу сказанного основу метода прогонки составляет так называемая прогоночная формула

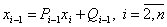(4.31)

где  – прогоночные коэффициенты. Для вычисления  используются следующие формулы:

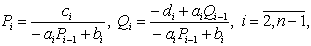	(4.32)
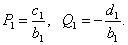	(4.33)

В прямой прогонке, как уже было сказано выше, последовательно находим  из (4.33),  из (4.32).