4.8. Вычисление определителей и обратных матриц

При решении системы линейных алгебраических уравнений методом Гаусса и его модификациями можно попутно вычислить определитель системы следующим образом.

В прямом ходе метода Гаусса матрица  системы (4.1) при условии, что ведущие элементы всех строк отличны от 0, приводится к треугольному виду. Последний получается после деления соответствующих строк на их ведущие элементы и последующего вычитания таких нормированных строк, умноженных на соответствующие числа, из других строк матрицы. При этом определитель матрицы тоже делится на соответствующий ведущий элемент, а последующие операции (умножения и вычитания) не меняют значения определителя матрицы  (см. [2, с. 146–147]; [6, с. 381]; [7, с. 283–284]).

В результате выполнения прямого хода схемы Гаусса получим систему (4.23) с треугольной матрицей, у которой определитель равен 1. Последний получается в результате деления  на ведущие элементы , т.е.

или

.

При решении системы методом Гаусса и его модификациями можно попутно вычислить определитель системы. Если стоит задача найти только определитель заданной матрицы , то вычисления проводятся по схеме, соответствующей прямому ходу метода Гаусса и его модификаций. При этом отсутствуют действия над столбцом правых частей системы. Число арифметических действий, выполняемых при вычислении определителя матрицы  с помощью этих методов, равно .

Замечание. В случае, когда при решении системы (4.1) применяется метод Гаусса с выбором главного элемента, или схема Жордана, рассуждая аналогично сказанному, получим, что в этом случае  равен произведению главных элементов.          

           Остановимся теперь на вопросе об определении элементов матрицы  (см. [2, с. 147–148]; [6, с. 379–380]; [7, с. 285–286]).

Пусть дана невырожденная матрица . Элементы обратной  матрицы будем обозначать . Очевидно, что

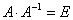(4.37)

где  – единичная матрица, т.е.

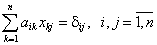(4.38)

Запишем (4.38) более подробно:

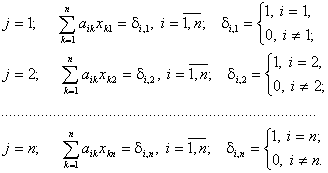
Получаем  систем из  линейных алгебраических уравнений, содержащих  неизвестных.

Все эти системы имеют одну и ту же матрицу  и отличаются между собой лишь свободными членами. В силу того, что при решении системы по методу Гаусса основные вычисления производятся над матрицей коэффициентов, то решение полученных  систем можно объединить в одной схеме и рассматривать одновременно  столбцов свободных членов. Естественно, что решение поставленной задачи предполагает использование ЭВМ.