4.9. Метод квадратного корня

В изложенных выше схемах метода исключения Гаусса можно сделать ряд упрощений, если матрица  исходной системы (4.1) является симметрической. Однако в случае симметрической матрицы удобным методом решения системы является метод квадратного корня (см. [4, с. 135–137]; [5, с. 99–101]; [6, с. 391–393]; [7, с. 287–290]).

Суть метода квадратного корня состоит в следующем. Пусть дана линейная система (4.1), где  – симметрическая квадратная матрица порядка , т.е.  – вектор правых частей системы,  – вектор-столбец неизвестных.

Решение системы (4.1) проведем в два этапа.

I этап (прямой ход). Согласно следствию из -теоремы представим матрицу  в виде

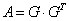(4.39)

где  – нижняя треугольная матрица,  – транспонированная по отношению к  матрица. Пусть

.

Тогда, производя перемножение матриц  и , получим следующие уравнения для определения элементов  матрицы :

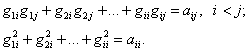(4.40)

Отсюда последовательно находим:

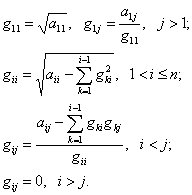(4.41)

Если , то

и система (4.1) имеет единственное решение.

Заметим, что при действительных  могут получиться чисто мнимые . Формально метод применим и в этом случае. Если же матрица  является положительно определенной, то мнимых  не будет.

II этап (обратный ход). В силу соотношения (4.39) система (4.1) эквивалентна двум системам с треугольной матрицей:

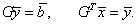(4.42)

Или в развернутом виде:

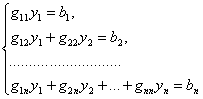(4.43)

и

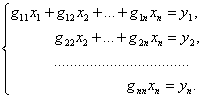(4.44)

Из (4.43) последовательно находим , ведя расчеты “сверху вниз” по формулам:

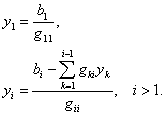(4.45)

Затем из (4.44) “снизу вверх” по найденным  последовательно находим , пользуясь формулами:

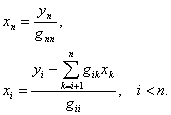(4.46)

При вычислениях по методу квадратного корня производится обычный контроль с помощью сумм, как и в методе Гаусса. При составлении сумм учитываются все коэффициенты соответствующей строки.

По сравнению с описанными выше методами решения систем данный метод дает выигрыш во времени в силу того, что:

1) существенно уменьшает число операций умножения и деления. По данному методу требуется произвести  операций извлечения квадратного корня (отсюда и название метода) и  операций умножения и деления (для больших  это почти в два раза меньше, чем в методе исключения Гаусса);

2) при расчетах на ЭВМ позволяет экономить память машины, т.к. матрица  – симметрическая. В вычислительной схеме можно записывать  верхних коэффициентов  и .

Кроме того, метод квадратного корня, как и изложенные выше методы, дает возможность найти . Для вычисления определителя достаточно провести прямой ход по формулам (4.41).