5.10. О скорости сходимости неявного метода простой итерации

Число итераций  в методе зависит от параметра , который подбирается из условия минимума числа итераций , при котором справедливо неравенство:

Здесь  – некоторый положительный и самосопряженный оператор.

Рассматривается неявная схема метода простой итерации:

где  – положительные, самосопряженные операторы. Заметим, что методы Зейделя и верхней релаксации не относятся к этому семейству схем, поскольку для них оператор  не является самосопряженным.

Введем обозначения: пусть  определяется по формуле:

поправка.

Тогда для  справедливо однородное уравнение:

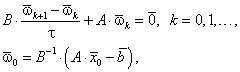(5.60)

где  – невязка,  – поправка.

Покажем это. Из неявного метода простой итерации определяется

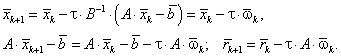
Из очевидного соотношения

следует (5.60).

Будем предполагать, что выполнены следующие операторные неравенства:

(5.61)

или

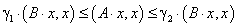(5.62)

для всех  где  – известные постоянные.

Приведем без доказательства теорему 10, позволяющую оценить скорость сходимости неявного метода простой итерации.

Теорема 10. Пусть выполнены условия (5.61), (5.62). Тогда минимальное число итераций по методу

достигается при

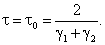(5.63)

При этом выполняется неравенство

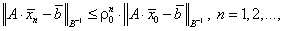(5.64)

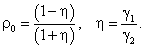(5.65)

Доказательство теоремы можно найти в [1, с. 107]. Там же получены оценки для числа итераций:

(5.66)

и более удобная для оценок формула

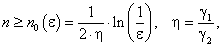(5.67)

причем , вообще говоря, нецелое.

Получим оценку числа итераций для явного метода простой итерации на следующей модельной задаче.

Рассмотрим систему линейных алгебраических уравнений вида

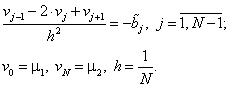(5.68)

Перепишем (5.68) в матричной форме:

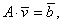(5.69)

где  – вектор размерности , а  – трехдиагональная матрица размерности :

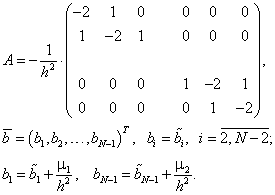
Матрице  из системы (5.69) соответствует оператор , действующий в пространстве  функций, заданных во внутренних узлах сетки  Если ,  , а  – функция, заданная на  и обращающаяся в нуль на границе сеточной области при  то

( – подпространство функций, заданных на  и обращающихся в нуль в граничных узлах ).

Вводя скалярное произведение в  аналогично [3, с. 108], можно показать, что  – самосопряженный, положительно определенный оператор, т.е. ,

 Кроме того, , причем

Для явного метода простой итерации  имеем:  . Тогда число итераций для этого метода оценивается следующим образом:

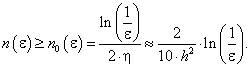
Если  Тогда  В частности, для  имеем , т.е. метод простой итерации существенно зависит от числа  разностных уравнений.

Задача (5.68) моделирует и более сложные случаи, т.к. аналогичное разностное уравнение соответствует уравнению Лапласа в двумерном и трехмерном случаях.

Замечание 1. Если  вычисляется через  и , то итерационный метод называется двухшаговым (или трехслойным). Примером такой схемы является трехслойная схема с постоянными параметрами: