5.11. Двухслойная итерационная схема с чебышевскими параметрами

Дано уравнение

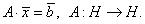(5.70)

Рассматривается итерационная схема с переменными параметрами :

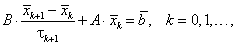(5.71)

для всех  Погрешность  и поправка  с начальным условием  удовлетворяют однородному уравнению

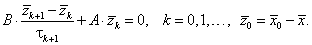(5.72)

Условие окончания итерационного процесса в (5.72) имеет вид:

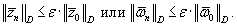(5.73)

Выразим  из (5.72). Получим

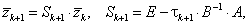(5.74)

где  – оператор перехода с -го на -й слой. Применяя рекуррентную формулу (5.74), получим:

Обозначим через  разрешающий оператор схемы (5.72). Тогда для

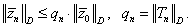(5.75)

Условие окончания итерационного процесса (5.72) будет выполняться, если

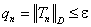(5.76)

Предположим, что в (5.71) матрица  – положительно определенная и для решения СЛАУ применим явный нестационарный итерационный метод Ричардсона

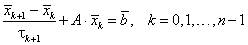(5.77)

где  – задан.

Укажем способ определения оптимального набора параметров , для которых  будет минимальна. Для этого сформулируем теорему.

Теорема 11. Пусть  – симметричная положительно определенная матрица, а  и  – ее наименьшее и наибольшее собственные значения. Пусть задано число итераций . Среди методов вида (5.77) наименьшую погрешность  имеет метод, для которого

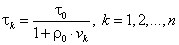(5.78)

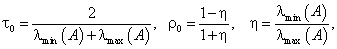(5.79)

Если выбирать  в соответствии с (5.78) и (5.79), то для погрешности будет справедлива оценка:

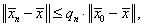(5.80)

где

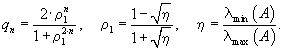(5.81)

Доказательство теоремы можно найти в [4, с. 108–109].

Итерационный метод (5.77) с параметрами , определенными в соответствии с (5.78), (5.79), называется явным итерационным методом с чебышевским набором параметров.

Отметим, что для  метод (5.77)–(5.79) совпадает с методом простой итерации

,

где .

Из теоремы 11 следует, что  является оптимальным значением параметра  в методе простой итерации. Для  оценка (5.80), (5.81) получается в виде:

Для любой n-й итерации справедлива оценка:

 или

Определим число итераций, при котором достигается заданная точность  в явном методе с чебышевским набором параметров. Из (5.80) следует оценка:

если , где  определяется в соответствии с (5.81). Итак, приходим к такому неравенству:

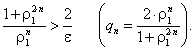(5.82)

Из (5.81) следует, что  тогда

Разрешая неравенство (5.82) относительно z, получим:

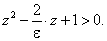(5.83)

Перепишем (5.83) в виде:

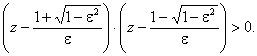
Отсюда следует,

что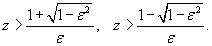

Очевидно, что если

, то, тем более

Последнее неравенство перепишем в виде

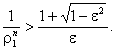
Оно будет справедливо, если потребовать

Откуда получаем, что

Для самого неблагоприятного случая, когда  мало, получается следующее неравенство:

Рассмотрим применение метода Ричардсона и метода простой итерации к ранее приведенной в п. 5.4 системе линейных алгебраических уравнений.

Пример 4.

Дана СЛАУ

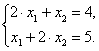
Матрица системы  – симметричная. Определим ее собственные значения из характеристического уравнения

Раскрывая определитель, получим:

Отсюда следует, что