5. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

5.1. Классификация итерационных методов. Исследование сходимости стационарных итерационных методов

Итерационные методы широко применяются при решении систем линейных алгебраических уравнений (СЛАУ)

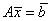(5.1)

где

В этих методах решение СЛАУ (5.1) с невырожденной матрицей  получается как предел итерационной последовательности , определяемой по формуле

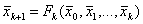(5.2)

где  – номер итерации, начальное приближение  – задано, а вектор-функции  определяют тот или иной итерационный метод и зависят, вообще говоря, от матрицы , вектора правой части  и номера итерации  (см. [1, с. 54–56]).

Определение 1. Если  не зависят от номера итерации , то итерационный метод называется стационарным (в противном случае – нестационарным).

Определение 2. Если функции  зависят только от  и не зависят от остальных приближений к решению , то метод называется двухслойным, или одношаговым или методом первого порядка (см. [1, с. 54]).

Наибольшее распространение на практике получили линейные стационарные методы первого порядка, представимые в виде

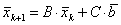(5.3)

где  – квадратные матрицы, связанные с исходной матрицей  некоторым соотношением. Выведем его.

Если рассматривать  как эквивалентную форму записи СЛАУ (5.1), то точное решение  должно удовлетворять эквивалентной СЛАУ. Тогда имеем

.

Отсюда получаем

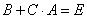(5.4)

Если в формуле (5.4) считать известной матрицу , то  будет определять множество итерационных методов решения СЛАУ (5.1) при различных . К настоящему времени широкое распространение получили следующие итерационные методы: Якоби, простой итерации, Зейделя, релаксации, Ричардсона и др. (см. [1-5]). Прежде чем обсуждать конкретные итерационные методы, остановимся на основных вопросах, которые приходится разрешать при использовании этих методов на практике:

1) каким образом задавать матрицу , и каким свойствам она должна удовлетворять?

2) каким следует выбирать начальное приближение ?

3) при каких условиях последовательность векторов  будет сходиться к точному решению ?

4) какой будет погрешность полученного итерационным методом приближенного решения?

Введем понятие сходимости итерационного метода.

Определение 3. Будем говорить, что итерационный метод сходится, если  при , где  – вектор погрешности приближенного решения , а под нормой понимается одна из норм векторов, согласованных с нормой матрицы  (см. [6]).

За сходимость итерационного метода (5.3) отвечает матрица , свойства которой определены теоремой (см. [1, с. 56–57]; [2, c. 105–107]).

Теорема 1. Стационарный линейный процесс

сходится при любом начальном векторе  и любой правой части  тогда и только тогда, когда все собственные значения матрицы  по модулю меньше единицы.

При доказательстве сформулированной теоремы потребуется несколько вспомогательных утверждений.