5.2. Метод Якоби

Пусть в системе (5.1) матрица  имеет вид:

где

,    ,

.

Предполагаем, что . Тогда СЛАУ (5.1) можно записать так:

или

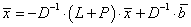(5.17)

Сравнивая (5.17) и (5.16), находим, что

На основе формулы (5.17) можно записать итерационный метод, который называют методом Якоби:

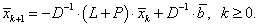(5.18)

Пусть . Тогда матричную формулу (5.18) с учетом вида матриц 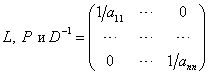 можно записать покомпонентно:

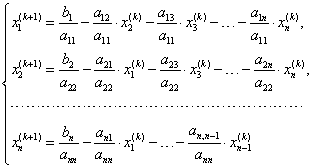
или

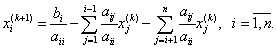(5.19)

Нетрудно видеть, что матрица В имеет представление:

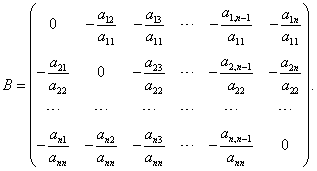
Согласно теореме 3 для сходимости метода Якоби достаточно, чтобы  была меньше 1. Если потребовать выполнения неравенств (5.13), то получим достаточное условие сходимости метода Якоби:

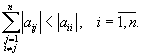(5.20)

Неравенство (5.20) означает диагональное доминирование в исходной матрице , которое достаточно для сходимости метода Якоби. Заметим, что диагонального преобладания в исходной матрице  следует добиться, прежде чем проводить вычисления по формулам (5.19). Поясним сказанное на примере.

Пример 1.

Пусть требуется методом Якоби найти решение СЛАУ с точностью ε:

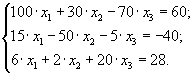(5.21)

Здесь

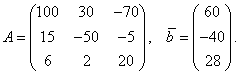
Точное решение 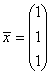, в чем можно убедиться непосредственной подстановкой его в СЛАУ.

Решение.

Так как в исходной матрице  диагонального преобладания нет (неравенства (5.20) не выполняются для первого уравнения), произведем подобные преобразования СЛАУ (5.21). Это можно сделать многими способами.

В рассматриваемом примере достаточно сложить первые два уравнения. Будем тогда иметь:

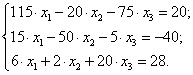
Итерационный процесс можно проводить по следующим формулам:

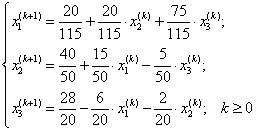
или

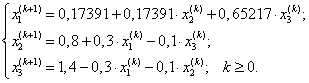
Выпишем вид матрицы :

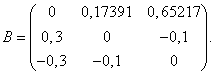
Несложно увидеть, что . В самом деле,

и

Таким образом, достаточные условия сходимости метода Якоби выполняются.

Положим

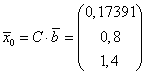
и получим несколько последующих приближений. Будем иметь:

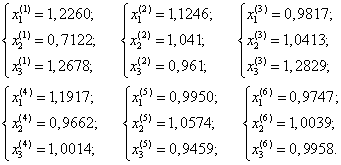
Приближения к точному решению рассматриваемой СЛАУ (5.21) различаются между собой на пятой и шестой итерациях в сотых долях, так что счет можно прекратить. Кроме того,

т.е. требуемые условия задания выполнены.

Установим теперь необходимые и достаточные условия сходимости метода Якоби. Согласно теореме 1 все собственные значения матрицы  должны быть по модулю меньше единицы. Это равносильно требованию: все корни характеристического уравнения

или

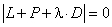(5.22)

должны быть по модулю меньше единицы. Уравнение (5.22) с учетом вида матриц  примет вид:

(5.23)

Таким образом, можно считать доказанной следующую теорему.

Теорема 5.

Метод Якоби (5.18) сходится к решению системы (5.1) тогда и только тогда, когда все корни уравнения (5.23) по модулю меньше единицы.