5.3. Метод Зейделя

В методе Якоби при получении компонент нового приближения  к искомому решению все вычисления в формулах (5.19) производятся через компоненты вектора , хотя при вычислении  уже найдено значение , а при определении  известны значения . Этот факт используется в методе Зейделя, который иначе еще называют методом Гаусса – Зейделя, или последовательных смещений. Выведем расчетные формулы метода Зейделя.

По-прежнему будем исходить из матричной формулы:

.

Предполагая, что , будем иметь:

или

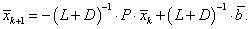(5.24)

Формула (5.24) есть матричная форма записи метода Зейделя. Сравним ее с матричной записью метода Якоби. Получим:

Тогда согласно теореме 1 для сходимости метода Зейделя необходимо и достаточно, чтобы все собственные значения матрицы  были по модулю меньше 1 или, что то же, все корни характеристического уравнения

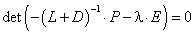(5.25)

были по модулю меньше 1.

Уравнение (5.25) эквивалентно следующему:

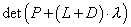(5.26)

Тогда справедлива следующая теорема.

Теорема 6. Метод Зейделя (5.24) сходится в том и только в том случае, когда все корни уравнения

(5.27)

по модулю меньше 1.

Запишем расчетные формулы метода Зейделя через компоненты векторов. Будем иметь:

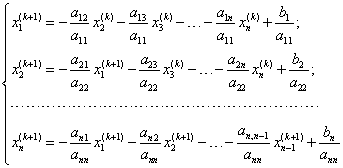
или

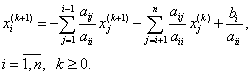(5.28)

Здесь  Вычисления по формулам (5.28) проводятся до тех пор, пока не будет выполнено условие:

,

где 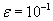 – принятая точность вычислений.

В методе Зейделя имеются достаточные условия сходимости:  Здесь под нормой понимается одна из норм матрицы.

Достаточные условия сходимости метода Якоби определяются неравенствами (5.20). При выполнении условий (5.20) сходится и метод Зейделя. Более того, он сходится быстрее, чем метод Якоби. Докажем это.