5.5. Единая каноническая форма записи итерационных методов

На примере метода простой итерации и метода Зейделя можно показать, что один и тот же итерационный метод можно записать различными способами. Поэтому имеет смысл ввести какую-либо стандартную форму записи итерационных методов.

В рассмотренной системе (5.1) будем считать  – линейным оператором в конечномерном пространстве  в котором определено скалярное произведение.

Введем так называемую единую каноническую форму записи для итерационных методов. Для любого двухслойного итерационного метода каноническая форма записи имеет вид:

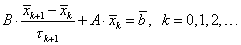(5.39)

для всех  Здесь  – номер итерации;  – начальное приближение;  – итерационные параметры,   – оператор из (5.1), а  – линейный оператор, имеющий обратный . Пусть для простоты  не зависит от номера итерации .

            Осуществим классификацию методов. Если  ( – единичный оператор), то метод вида

(5.40)

называется явным.

Для нахождения -го приближения к решению выразим  из (5.40):

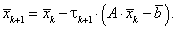(5.41)

В более общем случае, когда , метод (5.39) называется неявным итерационным методом. Для нахождения  используется уравнение

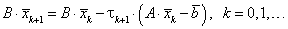(5.42)

Точность итерационного процесса (5.39) определяется величиной погрешности  где  – точное решение исходной СЛАУ. Подставляя в (5.39)  получим однородное уравнение для погрешности :

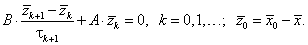(5.43)

Определение 4. Говорят, что итерационный метод сходится в , если  где  [3].

В процессе определения приближенного решения , как правило, задается некоторая погрешность  с которой надо найти приближенное решение . Вычисления прекращаются, если выполняется следующее условие:

(5.44)

Если  – наименьшее из чисел, для которых неравенство (5.44) справедливо, то общее число арифметических операций, требуемых для определения приближенного решения СЛАУ (5.1), определяется по следующей формуле:

Здесь  – число операций, затрачиваемых на выполнение одной итерации. Минимизировать  можно путем подбора матрицы  и параметров .

Рассмотрим простейшие итерационные методы, исходя из единой канонической формы (5.39).