5.7. Каноническая форма записи метода Зейделя

Этот метод достаточно широко применяется на практике, особенно тогда, когда информации о матрице  недостаточно. Приведем две формы записи метода Зейделя:

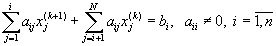(5.48)

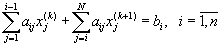(5.49)

Компоненты вектора  последовательно определяются из формул (5.48) и (5.49). Покажем, как это можно осуществить на примере формулы (5.48). Вначале находим , затем :

,

.

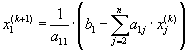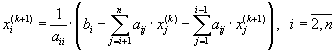Из (5.49) для  последовательно находятся:

,

.

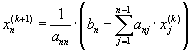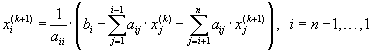Представим матрицу  в виде суммы трех матриц

,

где  – диагональная матрица размерности ,  – нижняя треугольная матрица (поддиагональная с нулями на главной диагонали), т.е.

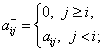
 – верхняя треугольная матрица, т.е.

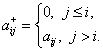
Тогда метод Зейделя можно записать в матричной форме. В самом деле, в силу определения  имеем, что

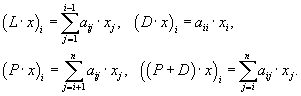
Тогда (5.49) можно переписать в виде

,

или в векторной форме

Очевидно, что

.

Используя последнее равенство, запишем метод Зейделя в канонической форме [3, c. 97]:

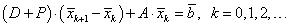(5.50)

Сравнивая (5.50) с канонической формой для любого двухслойного метода (5.39), нетрудно видеть, что методу Зейделя (5.50) соответствует

.

Последнее означает, что схема (5.50) является неявной. Так как  – треугольная матрица, то итерация  определяется по явной формуле.

Второй вариант метода Зейделя можно, по аналогии с предыдущим, записать в виде

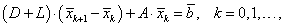(5.51)

если  – нижняя треугольная матрица.