5.9. О сходимости стационарных итерационных методов

Стационарным итерационным методом называется метод вида

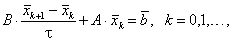(5.53)

в котором  не зависят от номера итерации  – задано.

К числу стационарных неявных методов относится и метод Зейделя, и метод релаксации.

Для существования обратного оператора  достаточно, чтобы оператор  был положительным. Пусть . Покажем, что  Если оператор  – положительный и самосопряженный, т.е. , то имеем . Кроме того, , следовательно,  или

Из последнего соотношения следует, что

Подставляя полученное выражение в формулу

будем иметь

если .

Для погрешности  справедливо однородное уравнение

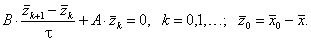(5.54)

Теорема 8. Пусть  – самосопряженный положительный оператор и выполнено условие

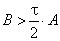(5.55)

Тогда итерационный метод (5.53) сходится в , т.е.

Доказательство теоремы можно найти в [3, с. 102–104].

Доказательство.

Воспользуемся разностным уравнением (5.54) для погрешности и подставим в него  В результате получим:

Умножим полученное выражение скалярно на

Тогда первое слагаемое примет вид:

Второе слагаемое, учитывая, что , можно записать следующим образом:

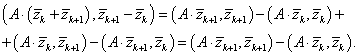
В результате получается энергетическое тождество:

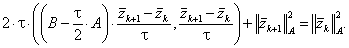(5.56)

Согласно теореме выполнено условие (5.55). Тогда первое слагаемое в левой части тождества (5.56) будет неотрицательно, и, отбрасывая его, получим следующее неравенство:

Отсюда можно записать такую цепочку неравенств:

из которой видно, что последовательность  – невозрастающая и ограничена снизу нулем. На основании теоремы Вейерштрасса  будет сходиться при .

Докажем далее, что . Рассмотрим оператор . Он положителен в силу (5.55). Оператор  (см. [1, с. 41]) положительно определен, т.е. существует такое , что

 для всех

Тогда из тождества (5.56) получается следующее неравенство:

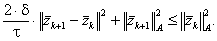(5.57)

Так как последовательность  сходится, то существует

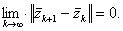(5.58)

С помощью (5.54) определяем:

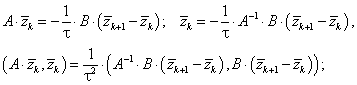
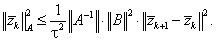(5.59)

Из последнего неравенства и из (5.58) следует, что

.

И теорема 8 доказана.

Замечание. Из неравенства (5.57) следует, что

Получим оценку для  из (5.59):

.

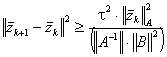С помощью последней оценки можно усилить предыдущее неравенство:

.

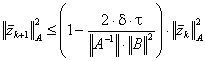Обозначим

.

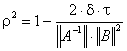Последнюю оценку перепишем в виде:

Выполнение этого неравенства означает, что итерационный метод (5.53) сходится при условии (5.55) со скоростью геометрической прогрессии.

С помощью теоремы 8 докажем сходимость ранее рассмотренных методов.