6. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ

6.1. Общие замечания. Сведения из алгебры

В данной главе рассматривается теоретически и практически важная задача линейной алгебры, называемая проблемой собственных значений и собственных векторов матриц.

Введем следующие определения.

Определение 1. Собственным значением (или характеристическим числом) квадратной матрицы  называется такое число , что для некоторого ненулевого вектора  имеет место равенство

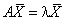(6.1)

Определение 2. Любой ненулевой вектор, удовлетворяющий этому равенству, называется собственным вектором матрицы , соответствующим (или принадлежащим) собственному значению .

Очевидно, что все собственные векторы матрицы  определяются с точностью до числового множителя.

Ценность сведений о собственных значениях матрицы  не вызывает сомнений. В самом деле, сходимость и скорость сходимости метода простой итерации, применяемого для приближенного решения системы линейных алгебраических уравнений

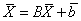(6.2)

существенно зависят от величины максимального по модулю собственного значения матрицы  (см. [3, с. 136]).

Заметим, что задача нахождения собственных значений и собственных векторов матрицы имеет значение не только как вспомогательная. Многие прикладные задачи физики, механики, астрономии, радиофизики приводят исследователя к проблеме определения нетривиального решения однородной системы линейных алгебраических уравнений вида (6.1) и тех значений числового параметра , при которых такое решение существует (см. [1, с. 219]).

Проблема собственных значений играет значительную роль во всех явлениях неустойчивых колебаний и вибраций, т.к. частота колебаний определяется собственными значениями некоторой матрицы, форму же этих колебаний указывают собственные векторы этой матрицы [1]. Анализ собственных значений матриц является важной темой научно-технических исследований.

Условием существования нетривиального решения у системы (6.1) (или, что то же, , где  – единичная матрица) является требование:

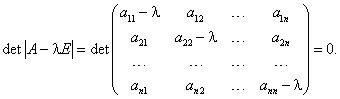(6.3)

Обычно это уравнение называется характеристическим (или вековым) уравнением матрицы . Левая часть этого уравнения

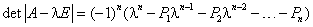(6.4)

называется характеристическим полиномом матрицы. Вместо полинома вида (6.4) рассматривают полином, отличающийся от характеристического множителем . Этот полином имеет вид

и обычно называется собственным многочленом матрицы. Собственные значения матрицы есть корни её собственного многочлена .

Совокупность всех собственных значений  матрицы , где каждое  выписано столько раз, какова его кратность как корня , называется спектром этой матрицы.