6.2.3. Метод вращений

Прежде чем привести общую схему метода вращений, а также QR-алгоритма, отметим, что основные понятия, используемые в этих методах, такие как ортогональная, эрмитова матрица, треугольная матрица, матрица отражений и другие, можно найти, например, в [5, с. 9–29]; [9, с. 265–267].

Среди итерационных методов особое место занимает метод вращений (метод Якоби) решения полной проблемы собственных значений вещественной симметричной матрицы (см. [5, с. 112]). Метод основан на построении последовательности матриц, которые ортогонально подобны исходной матрице и имеют монотонно убывающие до нуля суммы всех внедиагональных элементов.

Без существенных изменений метод вращений переносится на эрмитовы и косоэрмитовы матрицы.

Ограничимся рассмотрением случая вещественной симметричной матрицы . Случай комплексной эрмитовой матрицы можно посмотреть в [5, с. 126–127].

Итерационный процесс осуществляется следующим образом.

На 1-м шаге в матрице  определяется максимальный по абсолютной величине элемент . Далее строится матрица вращения:

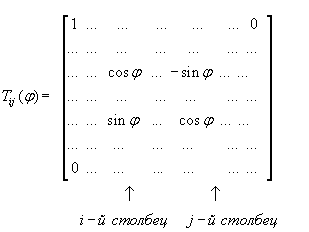
Угол  подбирается таким образом, чтобы у матрицы

элемент , обратился бы в нуль.

В целом метод состоит в построении последовательности матриц

каждая из которых получается из предыдущей при помощи шага, аналогичного вышеуказанному. Опуская для простоты записи индекс  у матрицы, исследуем результат преобразования

,

обозначая элементы матриц  и  через . Из формулы для  будем иметь:

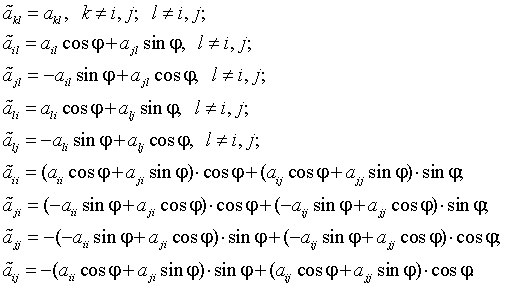
С учетом симметрии матрицы  легко проверить, что

Из последнего соотношения следует, что для уменьшения суммы квадратов внедиагональных элементов матрицу  необходимо выбрать таким образом, чтобы выполнялись два условия:

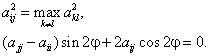
Из второго условия следует, что

Отсюда

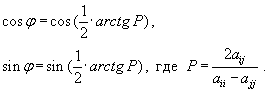
В [5, с. 23–29] доказано, что сходится к диагональной матрице  при . Тогда приближенными значениями собственных чисел матрицы  будут диагональные элементы матрицы , а приближенными значениями собственных векторов – столбцы матрицы (см. [5, с. 25–26]):

.