6.3.1. Нахождение максимального по модулю собственного значения
Допустим, что
квадратная матрица ![]() порядка
порядка
![]() обладает полной
системой
обладает полной
системой ![]() линейно
независимых собственных векторов
линейно
независимых собственных векторов ![]() соответствующих собственным значениям
соответствующих собственным значениям ![]() т.е. справедливо
т.е. справедливо
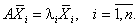 |
(6.7) |
Такой случай
возможен, когда все собственные значения различны между собой или матрица ![]() – симметричная.
– симметричная.
Пусть все ![]() упорядочены так, что выполняются неравенства:
упорядочены так, что выполняются неравенства:
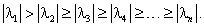 |
(6.8) |
Зададим произвольный вектор
![]()
и разложим его по векторам базиса ![]() . Имеем:
. Имеем:
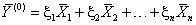 |
(6.9) |
С помощью вектора ![]() построим итерационную последовательность:
построим итерационную последовательность:
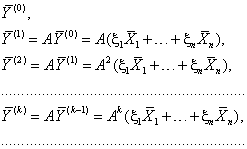 |
(6.10) |
Как следует из (6.7),
![]()
Тогда
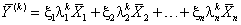 |
(6.11) |
Обозначим
![]()
Тогда векторное равенство (6.11) равносильно ![]() численным равенствам:
численным равенствам:
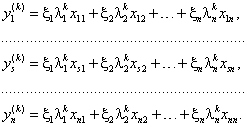 |
(6.12) |
Найдем, далее, отношения соответствующих
компонент вектора ![]() к
компонентам
к
компонентам ![]() .
Будем иметь:
.
Будем иметь:
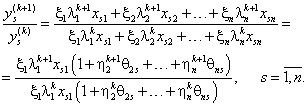 |
(6.13) |
Здесь введены обозначения:
![]()
Так как ![]() , то при
, то при ![]() из (6.13) получаем:
из (6.13) получаем:
![]() .
.
Следовательно, для достаточно больших ![]() можно приближенно принять
можно приближенно принять
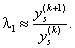 |
(6.14) |
Отметим, что все проведенные выше
выкладки справедливы в предположении, что ![]() . Обычно несколько компонент вектора
. Обычно несколько компонент вектора ![]() не равны 0. Тогда по
формуле (6.14) можно вычислить отношения при нескольких значениях
не равны 0. Тогда по
формуле (6.14) можно вычислить отношения при нескольких значениях ![]() . Если эти отношения
оказываются одинаковыми в пределах принятой точности вычислений, то счет
прекращают. При этом
. Если эти отношения
оказываются одинаковыми в пределах принятой точности вычислений, то счет
прекращают. При этом ![]() будет
найдено с некоторой заданной точностью.
будет
найдено с некоторой заданной точностью.
Изложенный
вычислительный процесс позволяет одновременно с наибольшим собственным
значением ![]() найти
соответствующий ему собственный вектор
найти
соответствующий ему собственный вектор ![]() .
.
В самом деле, из (6.11) имеем:
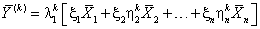 |
(6.15) |
Отсюда при больших ![]() следует, что
следует, что
![]() ,
,
т.е. собственный вектор ![]() определяется с точностью
до константы через
определяется с точностью
до константы через ![]() .
Если
.
Если ![]() , то
, то ![]() , а если
, а если ![]() , то
, то ![]() при
при ![]() . По этой причине векторы
. По этой причине векторы ![]() нуждаются в нормировке. Это можно
сделать несколькими способами. Например, вместо
нуждаются в нормировке. Это можно
сделать несколькими способами. Например, вместо ![]() можно строить последовательность векторов
можно строить последовательность векторов ![]() , где нормирующий множитель
, где нормирующий множитель
![]() , а
, а ![]() .
.