7. Лабораторный практикум
Лабораторная работа 1.
Цель: научиться решать алгебраические уравнения третьей степени.
Задание:
Пояснение:
1)Отделение корней алгебраического уравнения вида
![]()
осуществляется поэтапно:
а) ввод коэффициентов ![]() , варианты которых
приводятся ниже в табл. 7.1;
, варианты которых
приводятся ниже в табл. 7.1;
б) построение графика функции ![]() ;
;
в) определение промежутков ![]() ,
, ![]() , каждый из которых содержит
единственный корень уравнения.
, каждый из которых содержит
единственный корень уравнения.
Таблица 7.1
|
N |
a |
b |
c |
Кол-во вещ. корней |
|
1. |
-2 |
-1 |
1 |
3 |
|
2. |
2 |
-1 |
1 |
1 |
|
3. |
-2 |
-1 |
2 |
3 |
|
4. |
-3 |
1 |
3 |
1 |
|
5. |
-3 |
-2 |
3 |
3 |
|
6. |
3 |
-2 |
-3 |
3 |
|
7. |
1 |
-2 |
2 |
1 |
|
8. |
1 |
-1 |
-2 |
1 |
|
9. |
3 |
1 |
-3 |
1 |
|
10. |
3 |
1 |
-1 |
3 |
2) Нахождение одного вещественного корня
из промежутка ![]() с
точностью
с
точностью ![]() по
методу Ньютона:
по
методу Ньютона:
а) ввод ![]() ;
;
б) вывод последовательности приближений к корню
уравнения, числа итераций ![]() , для которого
, для которого![]() , и
, и ![]() .
.
3) Определение двух других корней уравнения аналитически:
а) получение квадратного
уравнения путем деления ![]() на
на ![]() ;
;
б) решение квадратного уравнения по теореме Виета;
в) сравнение найденных значений
корней со значениями с графика ![]() .
.
Программа для поиска корней уравнения методом Ньютона
Программа для поиска корней уравнения графическим методом
Лабораторная работа 2.
Цель: показать корректность постановки задачи решения СЛАУ, варианты которых приведены ниже. Вычислить решение системы. Расчеты проводить с тремя знаками после запятой.
Задание:
1) непосредственным развертыванием найти величину определителя матрицы;
2) вычислить обратную матрицу и определить решение системы ;
3) получить число обусловленности матрицы СЛАУ с использованием первой нормы;
4) сделать вывод о корректности постановки задачи решения СЛАУ.
Варианты заданий
№1
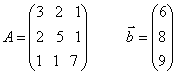
№2
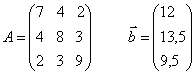
№3
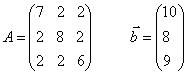
№4
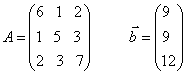
№5
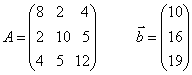
№6
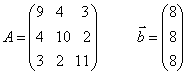
№7
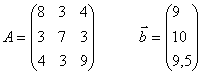
№8
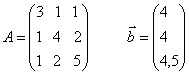
№9
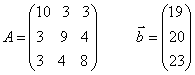
№10
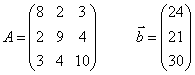
Проверка правильности решения