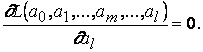2.3. ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ МОДЕЛИ

Задача параметрической идентификации сводится к отысканию таких оценок параметров модели, которые обеспечивают наибольшую, в каком либо смысле близость значений на выходе, рассчитанных по модели и, полученных в эксперименте, при одинаковом значении входных данных.

Рассмотрим модель с одним входом x  и одним выходом y. Пусть  проведено N опытов, в которых наблюдаемые на входе и выходе значения зафиксированы (см.таблицу 2.4).

Таблица 2.4.

x 1 Значение на входе, замеренное в 1-м опыте y 1 Значение на выходе, замеренное в 1-м опыте Значение, получаемое с использованием модели при том же входе: x 1 x 2 Значение на входе, замеренное в 2-м опыте y 2 Значение на выходе, замеренное в 2-м опыте Значение, получаемое с использованием модели при том же входе: x 1   и т.д.       x N-1 Значение на входе, замеренное в N-1 - м опыте y N-1 Значение на выходе, замеренное в N-1 - м опыте Значение, получаемое с использованием модели при том же входе: x 1 x N Значение на входе, замеренное в N - м опыте y N Значение на выходе, замеренное в N - м опыте Значение, получаемое с использованием модели при том же входе: x 1

В качестве критериев близости используются

1. Максимальное отклонение

   .

2. Среднее отклонение

   .

3. Стандартное или среднеквадратическое отклонение

   .

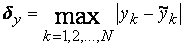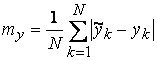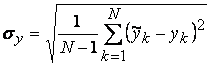Будем рассматривать линейные по идентифицируемым параметрам модели с n входами 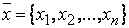и одним выходом: 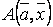. Т.е.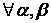 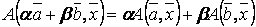 , здесь 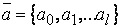, 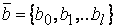- наборы параметров,  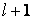число параметров, которые необходимо идентифицировать. Структурный вид оператора  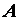представляется в этом случае так:  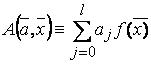, здесь 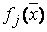- известные функции.

ЗАДАЧА 1.  Провести параметрическую идентификацию модели с 1-м входом x  и одним выходом y ,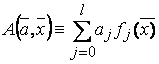, здесь 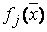- известные функции , 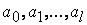- идентифицируемые параметры.

РЕШЕНИЕ:  Для идентификации модели проведем над моделируемым объектом 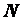 опытов, для каждого отдельного 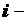- го эксперимента будем замерять значения на входе  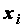и значения на выходе .

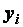В качестве критерия близости будем используют 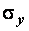- среднеквадратическое отклонение. Рассмотрим функцию
,   .

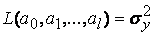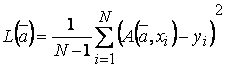Определим значения параметров из условия минимума функции 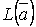 по допустимому множеству наборов параметров. Для отыскания набора параметров доставляющего минимум функции  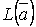можно использовать численные методы оптимизации.

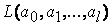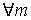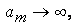
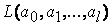
Метод наименьших квадратов. Заметим, что для линейных по идентифицируемым параметрам моделей функция  является положительно определенной  квадратической функцией своих аргументов и для  при   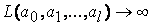 , следовательно, существует единственная точка минимума, которая может быть определена из решения системы уравнений:

. . .

. . .
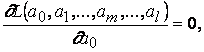
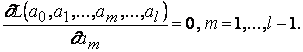