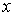 и одним выходом
и одним выходом 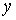 наиболее часто применяемые на практике.
наиболее часто применяемые на практике. Приведем примеры моделей с одним входом 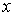 и одним выходом
и одним выходом 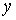 наиболее часто применяемые на практике.
наиболее часто применяемые на практике.
 - прямая;
- прямая;
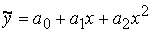 - квадратическая функция. График- парабола;
- квадратическая функция. График- парабола;
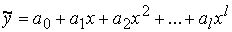 - полином общего вида;
- полином общего вида;
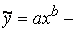 - степенной закон;
- степенной закон;
 степенной закон со сдвигом.
степенной закон со сдвигом.
ПРИМЕР 1. Провести параметрическую идентификацию модели с 1-м входом ![]() и одним выходом
и одним выходом ![]() , при условии, что
, при условии, что
![]() ,
,
здесь ![]() - идентифицируемые параметры.
- идентифицируемые параметры.
РЕШЕНИЕ. Для идентификации модели проведем над моделируемым объектом ![]() опытов, для каждого отдельного
опытов, для каждого отдельного ![]() го эксперимента будем замерять значения на входе
го эксперимента будем замерять значения на входе ![]() и значения на выходе
и значения на выходе ![]() .
.
Так как модель в нашем примере является линейной по своим параметрам ![]() , для решения задачи идентификации будем использовать МНК:
, для решения задачи идентификации будем использовать МНК:
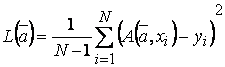 или
или
 .
.
Для определения параметров продифференцируем функцию ![]() по параметрам
по параметрам ![]() и получим систему
и получим систему

Преобразуем эту систему к виду
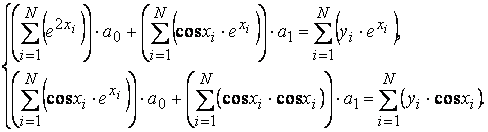
Решая систему, определяем параметры ![]() , например, по правилу Крамера
или методом исключения с использованием обратной матрицы.
, например, по правилу Крамера
или методом исключения с использованием обратной матрицы.
ПРИМЕР 2. Пусть в моменты времени ![]() замерялось давление в камере
некоторого устройства, результаты измерений сведены в таблицу
замерялось давление в камере
некоторого устройства, результаты измерений сведены в таблицу
|
|
|
|
|
|
|
|
|
|
Будем приближать зависимость давления от времени
многочленом. Для того чтобы, выбрать степень многочлена визуализируем
результаты измерения, изобразив их точками в плоскости ![]() (см. рисунок 2.4)
(см. рисунок 2.4)

Замечаем, что зависимость близка к линейной, поэтому
для приближения будем использовать многочлен 1-й степени ![]() .
.
Составим функцию 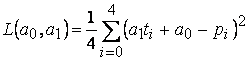 . Будем определять параметры, как решение
системы
. Будем определять параметры, как решение
системы
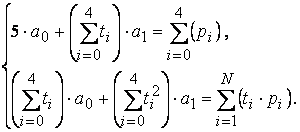
Подставим значения из таблицы и получим систему
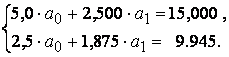
Решим систему и определим ![]() .
.