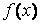 на множестве
на множестве 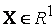 . Для этого сначала напомним основные
определения математического анализа [
. Для этого сначала напомним основные
определения математического анализа [ ].
].
Рассмотрим
задачу минимизации (поиска минимума) функции 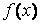 на множестве
на множестве 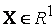 . Для этого сначала напомним основные
определения математического анализа [
. Для этого сначала напомним основные
определения математического анализа [ ].
].
 |
Определение 1.
Точка 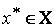 называется точкой локального минимума функции называется точкой локального минимума функции
где |
Точка ![]() называется точкой
глобального минимума, если неравенство (2.1) выполняется для всех
называется точкой
глобального минимума, если неравенство (2.1) выполняется для всех ![]() . Если неравенство (2.1) выполняется как строгое, то точка
. Если неравенство (2.1) выполняется как строгое, то точка ![]() называется точкой строгого минимума в глобальном или локальном смысле. Величину
называется точкой строгого минимума в глобальном или локальном смысле. Величину ![]() называют минимальным значением
называют минимальным значением ![]() на
на ![]() и обозначают
и обозначают ![]() .
.
Множество всех точек минимума ![]() на X будем обозначать
на X будем обозначать ![]() . В зависимости от свойств множества X и функции
. В зависимости от свойств множества X и функции ![]() множество
множество ![]() может содержать одну, несколько и даже бесконечно много точек, а также возможны случаи, когда
может содержать одну, несколько и даже бесконечно много точек, а также возможны случаи, когда ![]() пусто.
пусто.
В тех случаях,
когда ![]() ,
естественным обобщением понятия наименьшего значения функции является понятие
нижней грани функции.
,
естественным обобщением понятия наименьшего значения функции является понятие
нижней грани функции.
 |
Определение 2.
Пусть функция 1) 2) для любого сколь угодно малого числа ε > 0 найдется точка |
Если функция ![]() не ограничена снизу на X, то в качестве нижней грани
не ограничена снизу на X, то в качестве нижней грани ![]() на X принимается
на X принимается ![]() .
.
Нижняя грань ![]() на X обозначается через
на X обозначается через ![]() .
.
Если ![]() , то, очевидно, что нижняя грань
, то, очевидно, что нижняя грань ![]() на X совпадает с наименьшим значением этой функции на X, т.е.
на X совпадает с наименьшим значением этой функции на X, т.е. ![]() . В этом случае говорят, что функция
. В этом случае говорят, что функция ![]() на X достигает своей нижней грани.
на X достигает своей нижней грани.