2.4.2. Численные методы линейного поиска

Остановимся на  некоторых численных методах решения задачи минимизации для функции одной переменной. Для этого рассмотрим задачу минимизации функции

.

(2.4)

В том случае, если на интересующем нас промежутке функция  является дифференцируемой, то один из подходов решения поставленной задачи заключается в решении уравнения

.

(2.5)

Однако уравнение  (2.5) может быть нелинейным, или решение может быть точкой максимума или точкой перегиба. Если же функция  не имеет производной, то такой подход вообще не применим. Обычно при решении задачи минимизации функции одной переменной (2.4) избегают решения уравнения (2.5). Вместо этого используют некоторые численные процедуры находящие минимум функции.

Процедурой численного решения или численным алгоритмом нахождения решения задачи оптимизации называют итерационный процесс, который порождает последовательность точек в соответствии с предписанным набором правил, включающим критерий останова.

Линейный поиск - это процедура отыскания точек экстремума функции одной переменной.

Если функция - дифференцируемая, то процедуры линейного поиска могут использовать ее первую и вторую производные. Для некоторых классов функций разработаны численные методы, не использующие производную. Ниже дается определение строго квазивыпуклой функции многих переменных. Для функций этого класса, зависящих только от одной переменной, доказана теорема [], которая является основой большого количества методов линейного поиска.

Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы.- М.: Мир, 1992. - 584с. Полный список литературы

Определение 6. Пусть , где непустое выпуклое множество в . Говорят, что функция  строго квазивыпуклая, если  таких, что справедливо

Определение 7. Интервал  называется интервалом неопределенности, если точка локального минимума функции .

На рисунке 2.5 приведены примеры строго квазивыпуклых функций.

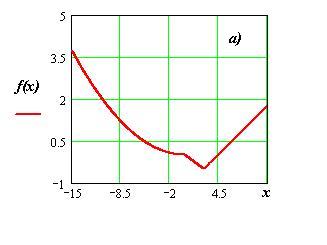
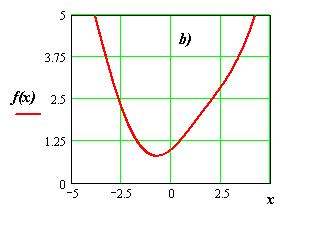Рисунок 2.6. Примеры строго квазивыпуклых  функций одной переменной