
Точка ![]() осуществляет
золотое сечение отрезка
осуществляет
золотое сечение отрезка ![]() , если отношение длины всего отрезка к длине большей его части равно отношению большей части к длине меньшей части:
, если отношение длины всего отрезка к длине большей его части равно отношению большей части к длине меньшей части:
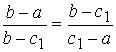 , при
, при ![]() ,
,
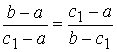 , при
, при ![]() .
.
 |
Определение 8.
Точка
|
Точка ![]() , симметричная точке
, симметричная точке ![]() относительно середины отрезка
относительно середины отрезка ![]() , является вторым золотым сечением этого отрезка. Из определения 8 следует, что
, является вторым золотым сечением этого отрезка. Из определения 8 следует, что
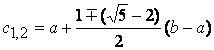 .
.Предположим, что на ![]() й
итерации интервал неопределенности равен
й
итерации интервал неопределенности равен ![]() , тогда новый интервал неопределенности,
согласно теореме 2, равен
, тогда новый интервал неопределенности,
согласно теореме 2, равен ![]() , если
, если ![]() , или
, или ![]() , если
, если ![]() . Будем выбирать новый интервал
неопределенности так, чтобы выполнялись следующие 2 условия:
. Будем выбирать новый интервал
неопределенности так, чтобы выполнялись следующие 2 условия:
A. Длина нового интервала неопределенности не зависит от того, выполняется
ли неравенство ![]() или
неравенство
или
неравенство ![]() ,
т.е.
,
т.е. ![]() .
.
B. Для новой итерации ![]() и
и ![]() выбираются так, чтобы либо
выбираются так, чтобы либо ![]() или
или ![]() .
.
Пусть точки ![]() и
и ![]() задаются по формулам
задаются по формулам
| (2.6) |
| (2.7) |
Здесь ![]() . Легко видеть, что
длина нового интервала неопределенности не зависит от того, какое неравенство
выполняется и равна
. Легко видеть, что
длина нового интервала неопределенности не зависит от того, какое неравенство
выполняется и равна ![]() ,
если точки
,
если точки ![]() и
и ![]() выбираются по формулам
(2.6)-(2.7). Определим далее, какое значение
выбираются по формулам
(2.6)-(2.7). Определим далее, какое значение ![]() нужно выбирать для того, чтобы выполнялось
условие В. Пусть
нужно выбирать для того, чтобы выполнялось
условие В. Пусть ![]() , т.е. новый интервал неопределенности
равен
, т.е. новый интервал неопределенности
равен ![]() или
или ![]() . Потребуем, чтобы
. Потребуем, чтобы ![]() . Согласно формуле
(2.6)
. Согласно формуле
(2.6)
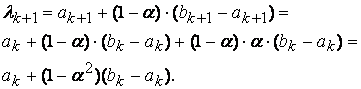
Рассмотрим ![]() . Приравняем
. Приравняем ![]() , получим
, получим ![]() .
.
Пусть ![]() , т.е. новый интервал
неопределенности равен
, т.е. новый интервал
неопределенности равен ![]() или
или ![]() . Потребуем, чтобы
. Потребуем, чтобы ![]() . Согласно формуле (2.7)
. Согласно формуле (2.7)
![]() .
.
Рассмотрим ![]() , приравняем
, приравняем ![]() , получим
, получим ![]() . Таким образом,
выбирая в качестве
. Таким образом,
выбирая в качестве ![]() положительный
корень этого уравнения (
положительный
корень этого уравнения (![]() ,
, ![]() ), построим процесс сокращения интервала
неопределенности удовлетворяющий условиям А и B.
), построим процесс сокращения интервала
неопределенности удовлетворяющий условиям А и B.