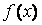1.2. Интерполяционный сплайн первой степени

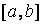При лагранжевой интерполяции в постоянные коэффициенты полинома вкладывается информация о неодинаковом (в общем случае) поведении функции 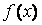на .

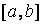Рассмотрим другой подход, основанный на кусочно-полиномиальной (сплайновой) интерполяции [13, 14, 15, 16].

Пусть на отрезке 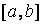вещественной оси 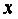задана сетка

.

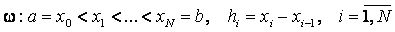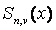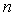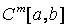
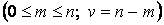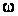Определение. Функция называется интерполяционным полиномиальным сплайном степени класса с узлами на сетке , если:

1.На каждом отрезке 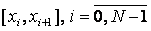 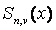является многочленом степени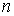

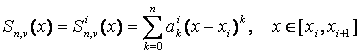(7)

2.

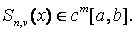(8)

3.

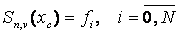(9)

Отметим, что узлы сплайна в (7) могут не совпадать с узлами интерполяции в (9), например, для четных n.

Определение. Число разрывных производных сплайна 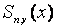во внутренних узлах сетки 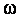называется дефектом сплайна и характеризуется индексом

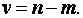
Как следует из этих определений, при интерполяционный сплайн первой степени дефекта 1 есть ломаная (см. рис. 6), для которой

Рис. 6

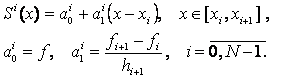
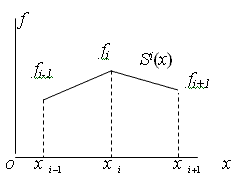
Иногда удобно пользоваться другой формой записи линейной функции:

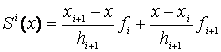(10)