1.7. Параметрические сплайны
Рассмотренные выше алгоритмы позволяют по
дискретному набору точек восстанавливать плоские кривые, которые имеют конечную
длину и описываются зависимостью вида
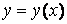 ,
,
 .
Однако так можно представить не все кривые. Наиболее универсальным способом их
задания является параметрический, который допускает представление замкнутых
кривых, кривых с самопересечением и т.д. В этом случае кривая
.
Однако так можно представить не все кривые. Наиболее универсальным способом их
задания является параметрический, который допускает представление замкнутых
кривых, кривых с самопересечением и т.д. В этом случае кривая
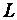 ,
которую можно представлять себе как траекторию непрерывного движения точки,
задается двумя уравнениями
,
которую можно представлять себе как траекторию непрерывного движения точки,
задается двумя уравнениями 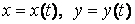 ,
где
,
где 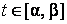 –
параметр,
–
параметр, 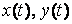 –
непрерывные функции. Например, для окружности
–
непрерывные функции. Например, для окружности
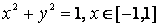 ,
параметрическое представление имеет вид
,
параметрическое представление имеет вид
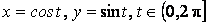 .
Отметим, что параметризация кривой
.
Отметим, что параметризация кривой 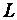 может
быть осуществлена различными способами, а параметрическое уравнение кривой в
векторной форме имеет вид
может
быть осуществлена различными способами, а параметрическое уравнение кривой в
векторной форме имеет вид
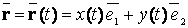 ,
,
где
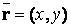 –
радиус-вектор текущей точки на кривой;
–
радиус-вектор текущей точки на кривой;
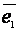 и
и
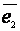 –
орты координатных осей. Для регулярной кривой
–
орты координатных осей. Для регулярной кривой
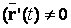 ,
,
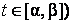 в
каждой её точке существует касательная, которая непрерывно меняется вдоль этой
кривой.
в
каждой её точке существует касательная, которая непрерывно меняется вдоль этой
кривой.
 |
 |
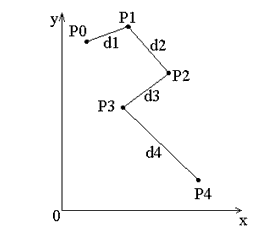
| Рис. 9 |
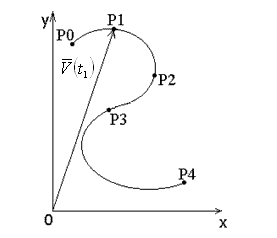
Рис. 10 |
Пусть на плоскости задан упорядоченный набор
точек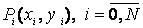 ,
и требуется восстановить кривую, проходящую через эти точки (рис. 9). По
,
и требуется восстановить кривую, проходящую через эти точки (рис. 9). По
точкам 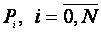 ,
построим контрольную ломаную, а в качестве параметра
,
построим контрольную ломаную, а в качестве параметра
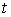 выберем
её длину, которая одновременно задаёт и ориентацию параметризованной кривой.
Тогда
выберем
её длину, которая одновременно задаёт и ориентацию параметризованной кривой.
Тогда
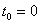 ,
,
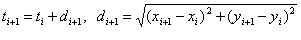 .
.
Учитывая выбранную параметризацию, получим две сеточные функции
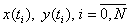 ,
по которым вычисляем, например, интерполяционные кубические сплайны
,
по которым вычисляем, например, интерполяционные кубические сплайны
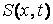 и
и
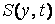 дефекта
1. При этом для незамкнутой кривой удобно использовать дополнительные условия
4-го типа.
дефекта
1. При этом для незамкнутой кривой удобно использовать дополнительные условия
4-го типа.
Совокупность этих двух функций
и будет являться интерполяционным параметрическим кубическим сплайном, векторная
форма которого имеет вид
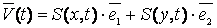 . . |
(88) |
Зная вектор-функцию (88), её можно уточнить, используя теперь естественную
параметризацию по длине дуги полученной кривой
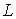 ,
изображённой на рис.10. В этом случае по формуле
,
изображённой на рис.10. В этом случае по формуле
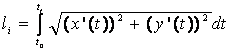 , ,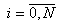 . . |
(89) |
определяется уточненный
массив параметризации 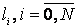 ,
для опорных точек
,
для опорных точек 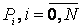 .
Теперь можно определить вектор-функцию второго приближения
.
Теперь можно определить вектор-функцию второго приближения
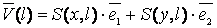 .
.
Отметим, что рассмотренный алгоритм легко обобщается на восстановление дискретно заданных пространственных кривых.
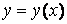 ,
,
 .
Однако так можно представить не все кривые. Наиболее универсальным способом их
задания является параметрический, который допускает представление замкнутых
кривых, кривых с самопересечением и т.д. В этом случае кривая
.
Однако так можно представить не все кривые. Наиболее универсальным способом их
задания является параметрический, который допускает представление замкнутых
кривых, кривых с самопересечением и т.д. В этом случае кривая
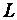 ,
которую можно представлять себе как траекторию непрерывного движения точки,
задается двумя уравнениями
,
которую можно представлять себе как траекторию непрерывного движения точки,
задается двумя уравнениями 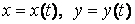 ,
где
,
где 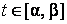 –
параметр,
–
параметр, 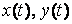 –
непрерывные функции. Например, для окружности
–
непрерывные функции. Например, для окружности
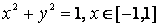 ,
параметрическое представление имеет вид
,
параметрическое представление имеет вид
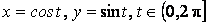 .
Отметим, что параметризация кривой
.
Отметим, что параметризация кривой 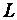 может
быть осуществлена различными способами, а параметрическое уравнение кривой в
векторной форме имеет вид
может
быть осуществлена различными способами, а параметрическое уравнение кривой в
векторной форме имеет вид
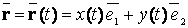 ,
,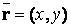 –
радиус-вектор текущей точки на кривой;
–
радиус-вектор текущей точки на кривой;
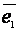 и
и
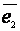 –
орты координатных осей. Для регулярной кривой
–
орты координатных осей. Для регулярной кривой
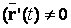 ,
,
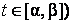 в
каждой её точке существует касательная, которая непрерывно меняется вдоль этой
кривой.
в
каждой её точке существует касательная, которая непрерывно меняется вдоль этой
кривой.


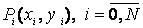 ,
и требуется восстановить кривую, проходящую через эти точки (рис. 9). По
,
и требуется восстановить кривую, проходящую через эти точки (рис. 9). По
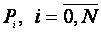 ,
построим контрольную ломаную, а в качестве параметра
,
построим контрольную ломаную, а в качестве параметра
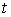 выберем
её длину, которая одновременно задаёт и ориентацию параметризованной кривой.
Тогда
выберем
её длину, которая одновременно задаёт и ориентацию параметризованной кривой.
Тогда
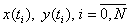 ,
по которым вычисляем, например, интерполяционные кубические сплайны
,
по которым вычисляем, например, интерполяционные кубические сплайны
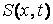 и
и
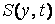 дефекта
1. При этом для незамкнутой кривой удобно использовать дополнительные условия
4-го типа.
дефекта
1. При этом для незамкнутой кривой удобно использовать дополнительные условия
4-го типа.
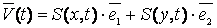 .
.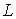 ,
изображённой на рис.10. В этом случае по формуле
,
изображённой на рис.10. В этом случае по формуле
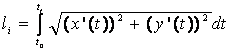 ,
,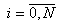 .
.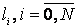 ,
для опорных точек
,
для опорных точек 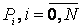 .
Теперь можно определить вектор-функцию второго приближения
.
Теперь можно определить вектор-функцию второго приближения
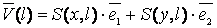 .
.