Определение.
Интерполяционный сплайн ![]() называется
кубическим нелокальным из
называется
кубическим нелокальным из ![]() ,
если:
,
если:
| 1. | 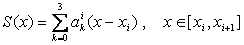 . . |
|
| 2. | 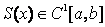 . . |
|
| 3. | 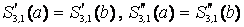 . . |
(90) |
где
 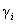 – заданные числа. – заданные числа. |
||
| 4. | 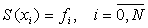 . . |
|
Для эрмитова кубического сплайна (43) с неизвестными
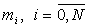 , имеем
, имеем
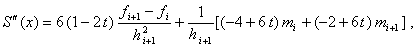 . . |
(91) |
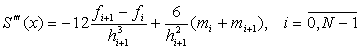 . . |
(92) |
С учетом формул (91) и (92) во внутренних узлах сетки для левых и правых производных получим
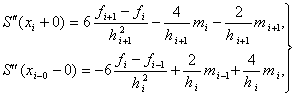 . . |
(93) |
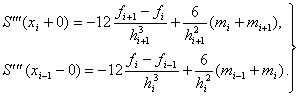 . . |
(94) |
Тогда система (90) имеет вид
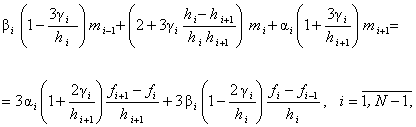 . . |
(95) |
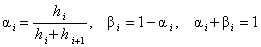 .
.