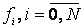 ,
степень интерполяционного многочлена равна
,
степень интерполяционного многочлена равна 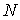 .
Пусть теперь на сетке
.
Пусть теперь на сетке 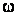 (см. рис. 1) необходимо построить интерполяционный многочлен
(см. рис. 1) необходимо построить интерполяционный многочленИзвестно [2],
что с ростом числа переменных процесс полиномиальной интерполяции
значительно усложняется. Поэтому, применяя выравнивающие переменные,
стремятся использовать многочлены невысоких степеней. Для сеточной функции
одной переменной 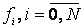 ,
степень интерполяционного многочлена равна
,
степень интерполяционного многочлена равна 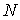 .
Пусть теперь на сетке
.
Пусть теперь на сетке 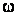 (см. рис. 1) необходимо построить интерполяционный многочлен
(см. рис. 1) необходимо построить интерполяционный многочлен
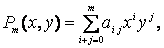 , , |
(22) |
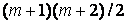 коэффициентов. Если при этом
коэффициентов. Если при этом 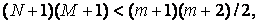 то часть коэффициентов в (22) приходится задавать, например, нулями.
Более того, если в одномерном случае достаточно, чтобы узлы
то часть коэффициентов в (22) приходится задавать, например, нулями.
Более того, если в одномерном случае достаточно, чтобы узлы
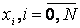 ,
были различными, то в двумерном случае для
,
были различными, то в двумерном случае для
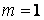 они не должны лежать на одной прямой
[4], а для
они не должны лежать на одной прямой
[4], а для 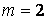 на одной кривой второго порядка и т.д.
на одной кривой второго порядка и т.д.
Пусть, как и в разд. 1.7, на плоскости задан упорядоченный набор
точек 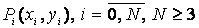 , и соответствующая
ему контрольная ломаная (ломаная Безье). Сглаживающая кривая Безье в векторной
форме, записанная по базисным функциям С.Н. Бернштейна [31], имеет вид
, и соответствующая
ему контрольная ломаная (ломаная Безье). Сглаживающая кривая Безье в векторной
форме, записанная по базисным функциям С.Н. Бернштейна [31], имеет вид
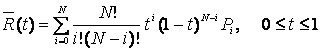 , , |
(23) |
Когда параметр 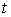 меняется от 0 до 1, кривая
меняется от 0 до 1, кривая 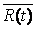 описывает на плоскости траекторию из точки
описывает на плоскости траекторию из точки 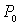 в точку
в точку 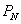 и расположена в выпуклой оболочке, порожденной массивом
и расположена в выпуклой оболочке, порожденной массивом 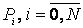 . Если точки
. Если точки 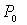 и
и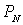 совпадают, то кривая замкнута. Для
совпадают, то кривая замкнута. Для 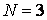 из (23) получим
из (23) получим
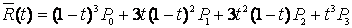 , , |
(24) |