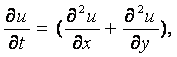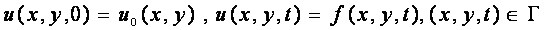.
.Для численного решения многомерных краевых задач активно используют метод конечных разностей, метод конечных элементов и метод конечных объемов [29].
Рассмотрим краевую задачу для двумерного уравнения теплопроводности
| . |
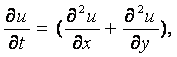(42) |
| . |
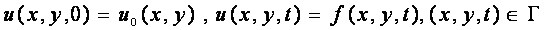(43) |
в области G={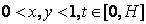
},
с границей 
,
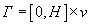где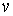 
- граница квадрата.
Применение явных схем приводит к достаточно простым расчетным формулам, но такие схемы условно устойчивы и для однопроцессорных ЭВМ относительно редко использовались. Ситуация изменилась с появлением многопроцессорных вычислительных систем, на которых явные схемы для линейных краевых задач легко реализуются и дают возможность получить решение за приемлемое время. Значительное число неявных схем является абсолютно устойчивым, либо эти условия более слабые, чем для явных схем. Это способствует большой популярности таких схем, особенно для нелинейных краевых задач.
Для задачи (42)-(43) запишем неявную схему метода последовательной сплайновой интерполяции [49]
  , |
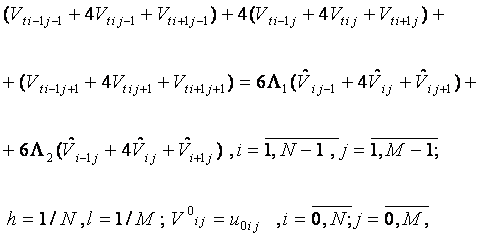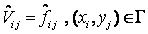(44) |
где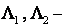 
разностные операторы второй производной по 
.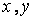